A Prototypical Point of View

According to prototype theory, categorization is accomplished by the acquisition of a prototypical representation of a category via a form of abstraction process. The prototypical representation is assumed to be a summary representation that corresponds to the 'central tendency', such as the arithmetic mean (Posner, 1969) or the mode (Neumann, 1977), of all the exemplars that have been experienced. New exemplars can then be classified on the basis of their similarity to this 'best example'. Consider, for example, what happens when one is asked to imagine a category such as 'tree'. Usually a typical instance of this category is immediately called to mind. The experimental investigation of this prototype effect began with Attneave (1957), and lead to the prototype view becoming as firmly established in the field of human cognitive psychology as exemplar or feature theories (see Smith & Medin, 1981; Medin & Smith, 1984; Homa, 1984, for a review).

In contrast, evidence in support of the prototype theory is rather poor and contradictory in pigeons. While the first attempts to demonstrate prototype effects produced negative results (Pearce, 1989; Watanabe, 1988), more recent attempts yielded positive findings (Aydin & Pearce, 1994; Huber & Lenz, 1996; White, Alsop & Williams, 1993). However, this does not warrant the conclusion that pigeons are able to abstract prototypes. There is also little agreement concerning the specific type of representation involved in prototypical categorization, and the specific conditions that facilitate categorization. The common denominator for all research in this field is a demonstration of the prototype effect. The prototype effect refers to the fact that the prototype, or exemplars that bear a close resemblance to it, are instantaneously classified. Sometimes even more readily than those exemplars of the same category that have already been experienced.

In an experiment, which we conducted to investigate this issue (Huber & Lenz, 1996), our primary aim was to determine what conditions facilitate prototype formation, rather than to provide empirical support for the

Pigeons appear unable to abstract prototypes in this manner. After having successfully discriminated triangular patterns of dots, of a given distortion level, from arbitrary dot patterns, the pigeons responded to a novel complete triangle less, rather than more, vigorously (Watanabe, 1988). Note that this behavior can easily be described as generalization from S+. Pearce (1989), who required pigeons to discriminate between artificial polymorphous classes comprised of 'histogram patterns', has provided further negative evidence. Three vertical bars, of varying heights, were used as the defining feature dimensions, in that their combined height defined their category membership. Pigeons that were trained on patterns with the combined height of 15 and 9 were then tested with those patterns that corresponded to the class average and patterns that corresponded to the extremes of the short-tall continuum. In contrast to the predictions of prototype theory, the pigeons' spontaneous classification of the extreme patterns was superior to that of the prototype patterns.

The same pattern of results, namely greater responding to extreme values than to any other instance along a continuum from positive to negative classes, was also found in our faces study (Huber & Lenz, 1993), and in von Fersen and Lea's (1990) study. In principle, this pattern of results also corresponds to the 'super-releaser effect' found in many classical ethological examinations of the sign stimulus eliciting fixed-action patterns (e.g., Tinbergen, 1951). We have interpreted this 'supernormal stimulus effect' in terms of feature learning, rather than in terms of the acquisition of an abstract representation of the category. However, those experiments, in which extreme values of the underlying feature rule failed to evoke 'supernormal' classification behavior (cf. Jitsumori, 1993; Lea & Harrison, 1978), have also failed to show any signs of a prototype effect. Therefore, they have been more parsimoniously explained in terms of learning about the entire patterns or some combination of features.

We suggested that the abstraction of prototypes is facilitated only when polymorphous stimulus classes are composed of many similar stimuli that share a "point of departure" or origin, but that cannot be separated in terms of the simple combination of feature dimensions. We sought to design a prototypical categorization task that fulfilled both of the following requirements:

The first requirement can be satisfied by designing stimulus classes that have features in common, but occupy regions in a multidimensional stimulus space that are not linearly separable. For instance, one cannot decide--as in the Huber and Lenz (1993) study--whether a Brunswik face is positive by summing up the values of the eye, brow, nose, and chin feature. The classes were designed using a distortion principle and thus occupied highly overlapping regions in the multidimensional feature space. Because the experimental design should favor the abstraction of categorical information rather than learning individual instances by rote, however, classification had to be facilitated on the basis of the central tendency of the global stimulus distribution. In other words, correct classification decisions should be determined not by reference to an undetermined number of previously experienced training stimuli (exemplar view) but by reference to the class prototype. A popular formulation of the latter strategy is the "distance rule of classification" (Posner, 1969; but also see Reed, 1972). According to this rule, in our study (Huber & Lenz, 1996) the criterion for class membership was the differential similarity distance from the prototype (that I shall label in geometric terms "radius"), measured by summing up the differences on every feature dimension. Positive stimuli are equally similar and close to

the prototype; negative stimuli are equally dissimilar and far from it. If imagined in three-dimensional space, the stimulus classes might be seen as hollow concentric spheres with different radius lengths around a common center (Figure 18).Despite the typicality structure of the stimulus space, pattern learning is still possible. Only a kind of trial-unique stimulus presentation design (Bhatt et al., 1988; Wright et al., 1988), in which the repetition of stimuli during training is minimized, is likely to inhibit pattern learning. We, therefore, created a stimulus library that includes several thousands of patterns. In order to enable the results of this experiment to be compared with those of Huber & Lenz (1993), we used the same stimuli as in our former study, but only increased the degree of variability.

The distortion rule to create two 'prototypical' categories

In Huber and Lenz (1993), each of the features eye, brow, nose, chin of the Brunswik faces could take on one of three values (-1, 0, +1). Here (Huber & Lenz, 1996), each feature could take one of nine values (-4 to +4), and also differed on each dimension in equal steps. This procedure generated 6561 (94) different patterns. As in the classical prototype studies, the primary criterion for class assignment was the similarity distance of a pattern from the prototype (P) or, in the language of standard terminology, the distortion level. Distortion levels were manipulated by varying the similarity distance between sets of stimuli and a chosen prototype. Similarity distance was defined by the additive combination of the difference between the values of all four feature dimensions (a city block metric). For example, when comparing a pattern containing the medium value on each dimension (i.e., 0, 0, 0, 0), with one containing extreme values (i.e., +4, -4, +4, -4), we obtain the a priori overall similarity by summing the absolute difference between each dimension (i.e., |4| + |4| + |4| + |4| = |16|). Using this 'transparent' distortion procedure, we were able to specify 'distortion' according to well-known feature dimensions, rather than by arbitrarily moving dots. In other words, it was possible to compare two faces by finding that one has, for example, a larger nose and more closely spaced eyes than the other, rather than by comparing two arbitrary dot patterns. I will return to this issue later when discussing our findings.

The positive category (POS), in which all stimuli were positively correlated with reinforcement, was defined by a distance equal to 4 (according to our similarity measure, see sidebar). The negative category (NEG), in which all stimuli were negatively correlated with reward, was defined by a distance equal to12. As a result of selecting two different patterns as prototypes, slightly different categorization tasks emerged. For one group (the Prototype Identical Group, PIG), the prototype was designated as 0, 0, 0, 0. If we average across all positive stimuli shown in training (n=192), as well as across all negative stimuli shown in training (n=528), the resulting arithmetic mean is identical for both classes, namely again 0, 0, 0, 0. For the other group (the Prototype Different Group, PDG), the prototype was designated as -2, +2, +2, -2. As a consequence of the asymmetrical feature distribution in the second group (a lower frequency of negative values for the features eye and chin and a higher frequency of positive values for the features brow and nose), averaging across the feature dimensions of all negative patterns shown in training (n=607) resulted in an arithmetic mean that was slightly different than that of the positive category (n=164). This enabled us to investigate whether it is easier to divide classes on the additional information of different prototypes than on the differing distance from a single prototype alone.

Training involved the presentation of arbitrarily chosen members of the two distortion levels. The implementation of a random generator function in the program that created and presented the faces permitted the use of a presentation order that was out of the control of the experimenter. The difficulty of this task meant that the training of the five pigeons lasted several months. Therefore, a high number of the stimuli from each category (several hundreds) were shown to the birds. The discrimination procedure used was in general the same as that used by Huber and Lenz (1993).

In contrast to all the birds used in the former study, only three of five pigeons achieved a satisfactory discrimination level (r = 0.8) within 50 sessions of 40 trials each. The two subjects that failed to solve the original classification task were subjected to a single-negative condition involving a single negative pattern rather than a negative class comprised of hundreds of patterns. This task was quickly solved.

The most interesting part of this experiment was the birds' performance during

generalization tests, which involved patterns that varied according to their distance from the prototype. Inspection of Figure 19 suggests the task to be a middle-value discrimination representing a band of positive stimuli surrounded by a band of negative stimuli on a single dimension. The most interesting question concerned the form of the generalization slope at the stimulus region inside category POS. A prototype effect (but also a peak shift effect, see below) would occur if the slope continues to rise in the center of the distance dimension, whereas orderly generalization around S+ would be found if the

slope falls. In Figure 20, the peck rate to individual stimuli is plotted against their distance from the prototype (radius). In contrast to the findings of Watanabe (1988), stimuli positioned close to the prototype (marked in red) elicited even more responses than the positive training stimuli at Radius 4. More generally, according to the distance-from-prototype model, there is a significant negative correlation between response rate and radius; the greater the difference between the transfer stimuli and the prototype, the less frequently the subjects pecked at the response key. This extremely orderly correlation (Pearson product-moment correlations between -0.906 and -0.975) confirms that a large proportion of the variance in pecking rate could be accounted for by its linear relationship with the distance dimension.

As in our former study, how strongly the individual face features controlled classification performance merits attention. This is particularly valuable with respect to the Prototype Different Group. In this group, the different prototypes to which the classes were anchored led t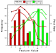

o the unequal distribution of feature values across classes (see the colored bars in Figure 21). Consequently, there was a strong correlation between class membership and attribute values. For example, a negative value for features 'e' and 'c' occurred approximately 1300 times in instances of the positive class, whereas a positive value for these features occurred only about 50 times as a signal for food. Simple linear feature rules, such as "if eye distance is short then peck", would make category discrimination possible. By and large, the combination of only two such feature rules would guarantee significant (r>0.68) classification ability.

Control of the pigeons' pecking behavior by independent features was examined by analyzing response rates to stimuli as a function of their feature value (see the colored lines in Figure 21). As found in the previous study (Huber & Lenz, 1993), a linear feature model predicts a linear relationship between response rate and feature value, with extreme values eliciting both the highest and the lowest number of pecks. In contrast, a prototype model would predict that responding would be most pronounced in the presence of the prototypical feature attributes (for Bird CG2 the values -2 and +2, respectively). Clearly, the data support a prototype model rather than a feature model.

Interestingly, the pecking behavior of the subjects that were successfully trained

with a single negative pattern (SNG) produced a different pattern of results (Figure 22). In contrast to the subjects of the Category Group, classification can be best described in terms of a linear feature rule; responding was most pronounced in the presence of the extreme (-4 and +4, respectively), rather than the prototypical, values. These different findings alone confirm the importance of considering category structure as an essential factor in categorization.

In our original paper (Huber & Lenz, 1996) we argued at some length that all three models of human categorization could account for some part of the present findings. Let me summarize the advantages and disadvantages of each theory.

The clearest evidence for feature learning comes from the birds belonging to the Single Negative Group. A linear feature mechanism of categorization easily accommodates their performance. The birds learned to combine--in additive manner--the information from all four feature dimensions until their judgments corresponded to a discriminant function that accurately predicted class membership. The ease with which these previously unsuccessful birds solved this task suggests that classes separated by a linear discriminant function are easy to identify. The pattern of responding shown by the remaining birds in this study also fits with the basic tenets of feature theory. Classification behavior may be correlated, not with the features as dimensions, but with the reinforcement rates of their discrete values. In order to explain the bell-shaped generalization functions around the prototypical feature attributes (see Figure 21) it is only necessary to consider that the prototypical feature attributes on each dimension are those that have occurred most frequently on reinforced trials, whereas the remote values on each dimension are correlated with non-reinforcement. This explanation is not only consistent with the Rescorla-Wagner (1972) theory, but also with frequency theories of feature abstraction and concept learning in the human literature (e.g. Goldman & Homa, 1977; Neuman, 1974).

As in the case of feature theory, the amount of data that can be explained by the exemplar view depends upon which version is applied. The simple notion that a novel stimulus is classified on the basis of its degree of similarity to all stored training stimuli is hard to defend, since the multidimensional average of the positive class was either identical (PIG), or highly similar (PDG), to the average of the negative class. This means that comparisons would balance out and the classes would become indiscriminable. A modified exemplar view based on Pearce's configural theory can also account for the present findings in much the same way as it accounted for Aydin and Pearce's (1994) findings. It rests on the possibility that an increased response rate to novel stimuli near the positive prototype may be caused by decreased inhibitory generalization from members of the nonreinforced category. The contrary effect, namely a reduction in response frequency during novel stimuli more distant from the prototype than the negative training patterns, may be caused by a loss of excitatory generalization. Following Spence's (1937) theory of gradient interaction, the prototype effect may be caused by a peak shift (Hanson, 1959; Purtle, 1973; Rilling, 1977).

The peak shift effects reported in the literature, however, clearly indicate that the distance over which the generalization peak shifts away from the S+ value, is rather short. While it may be difficult to estimate whether the prototype value lies within this distance, a negative peak shift is clearly absent. For both birds, CG2 and CG6, the decreasing trend of response rates away from S- (marked green in Figure 20) continued more than twice the distance between S- and S+ (marked blue). Finally, the generalization gradients found in the present study were quite different from the ones obtained by Watanabe (1988) in a similar experiment. If generalization from stored S+ and S- exemplars is a general classification strategy for pigeons, then why did Watanabe's pigeons not demonstrate a steady response increase towards the prototype?

A more coherent account of the transfer performance of the three successful birds is offered by prototype theory. We only need to propose the acquisition of a linear distance rule as a predictor of class membership in order to explain the strong correlation between distance from the standard pattern and response rate. Furthermore, this model is the most parsimonious in terms of memory load and most economical in terms of determining membership. A pigeon must keep in memory, for comparison with a novel unseen exemplar, only the (single) representation of the central tendency of the previously experienced class instances. In conclusion, this dual classification mechanism will cope easily with large, open-ended stimulus classes that show a polymorphous and typological (dense center--sparse periphery) structure.