Geometry, features, and orientation in vertebrate animals: A pictorial review
Ken Cheng and Nora S. Newcombe

Introduction: Modularity

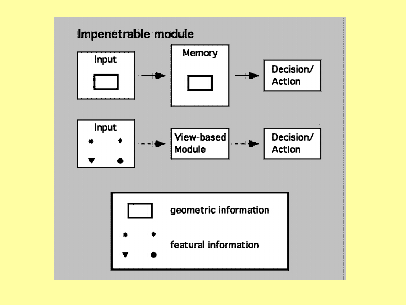
The following pictures, adapted from Figure 3 of Cheng and Newcombe (2005), show 3 views of modularity that we can identify. Doubtless there are other versions. These views concern modularity in the central system(s) that represent information. We consider below a notion of modularity at output.
 
In all three views, we have characterized the input processes as modular. Thus, we assume that different visual ‘channels’ handle and compute geometric and featural properties, a view consistent with Fodor (1983). In fact, visual systems are far more modular than the two boxes shown in the following three pictures (Marr, 1982).
 
Figure A-1:
In a strong view of modularity (Wang & Spelke, 2002, 2003), geometric information goes through an impenetrable module that handles only geometric information. “Impenetrable” means that the module does not admit any other kind of information.
 
 

 

Featural information, if it is used, is handled by other modular systems. We have listed a view-based module as one example. Thus, the systems run parallel through central processing to action.

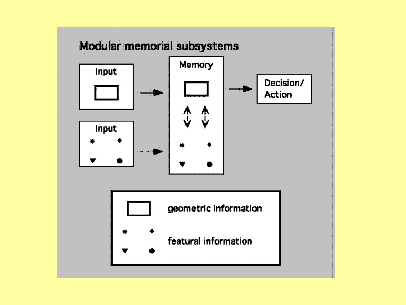
Some process uses only the geometric route. In Wang and Spelke (2002), it was the process of determining direction after disorientation. In Wang and Spelke (2003), it was either the process of determining direction or the process of locating a point in space after determining direction. We found the writing ambiguous (see Cheng & Newcombe, 2005, for a fuller discussion).

 

Figure A-2: A view of modular subcomponents in the central system characterizes Cheng’s (1986) discussion.

 

 

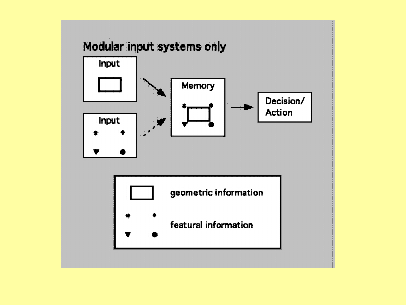
Note that we have drawn one memory box, in which both geometric and featural information are contained. Hence, this view differs from Wang and Spelke’s (2002, 2003) views. But there is some modularity in the central system, in that the geometric information is one submodule, the primary one. Cheng (1986) called it a geometric frame. It encodes the broad shape of the environment. (In the theory section, we report evidence indicating that animals may encode far less than the shape.) On this frame, crucial featural information may be pasted.
 
Rotational errors ensue when featural information fails to be entered at all (learning failure), or fails to be pasted on the geometric frame.

Figure A-3: In a completely integrated view (Newcombe, 2002), featural and geometric information are encoded together in the central system.
 

Their use may be weighted by many factors, including reliability of information, stability of landmarks, etc. Rotational errors ensue when featural information is either not entered at all into the central system (learning failure), or if they are weighted very little (e.g., because they are thought to be unreliable).

 

Modularity at output

A different kind of modularity concerns the use of information in guiding action, modularity at output.

 
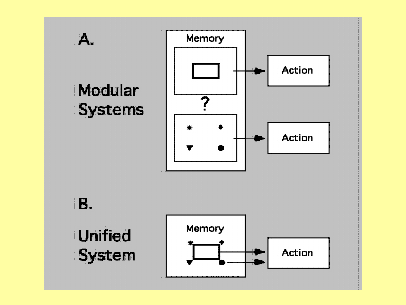
Figure A-4: In A., different kinds of information guide action separately. They do not interact.  In B., different kinds of information guide action together. The information is integrated at output. We have shown geometric and featural information in this picture, but the same notion also applies to other kinds of information.
 
 

Here, we are not concerned with how information is centrally organized (the ? in Figure 4A reflects this uncertainty), but with whether different kinds of information are integrated at output.

 
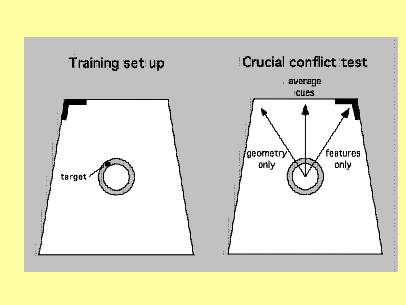
Figure A-5: This idea of modularity at output is best explained with concrete experimental examples. In the training set up here (left) the search space is the gray ring. The searcher has the problem of determining direction: at which direction from the center of the ring to search at. Around the ring are distant cues for direction determination. We assume that the animal is disoriented, but it has unambiguous geometric cues (the trapezoidal arena) and a featural cue at the top left corner.
 

After sufficient training, the cues are put in conflict. The featural cue is moved to the top right corner.

Arrows indicate interesting theoretical possibilities. The animal might rely completely on geometric information (left arrow). It might rely completely on the featural cue (right arrow). It might vacillate between the locations dictated by the geometric and the featural cues. Or, it might average the dictates of geometric and featural cues, and search somewhere between the right and left arrows.


This last outcome indicates integration of geometric and featural information at output.

The vacillation outcome is ambiguous. It might result from the existence of competing modules, or it might occur with integrated representations if the animal computes degree of match between competing locations and finds two imperfect matches.

 
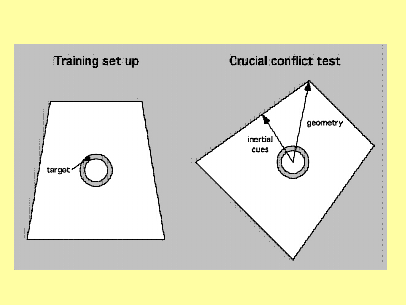
Figure A-6: This conceptual paradigm is not limited to geometric and featural cues. Consider for example an oriented animal trained in the training set up on the left. Its inertial sense of direction and the geometric cues of the trapezoidal arena both give directional cues.
 

In Figure 6, the two kinds of cues are put in conflict on the right, when the trapezoidal space is rotated in Earth-based coordinates. This puts geometric and inertial cues in conflict.

 

Thus, many kinds of cues can be tested in this fashion. One recent theory of the evolution of spatial cognition (Jacobs & Schenk, 2003) suggests that a part of the hippocampus is devoted to determining bearing or direction. If we read these authors right, this bearing system would use all available directional cues in an integrated fashion.

 

©2005 All copyrights for the individual chapters are retained by the authors. All other material in this book is copyrighted by the editor, unless noted otherwise. If there has been an error with regards to unacknowledged copyrighted material, please contact the editor immediately so that this can be corrected. Permissions for using material in this book should be sent to the editor.