Geometry, features, and orientation in vertebrate
animals: A pictorial review
Ken Cheng and Nora S. Newcombe
Macquarie University & Temple University
Artificial Intelligence
A check on recent citations reveals three different sources in the literature on artificial intelligence that have cited Cheng’s (1986) paper. Two take the notion of encoding geometry seriously, while one demonstrates how a robot may perform without encoding geometry.
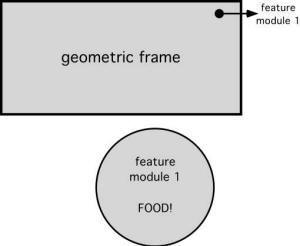 |
| Figure H-1: Egerton et al., 2000 |
Egerton, Callaghan, & Chernett (2000) took the idea of a geometric module or geometric frame to heart. They suggest a division of labor in encoding spatial information. A geometric frame or module encodes the broad shape of the environment. On it are pointers to feature modules. Feature modules tell about what is to be expected at a particular place or region in space. This picture shows a single feature module, but a functioning system would have a substantial bank of features.
A key point of this separation is to help solve what is called the problem of perceptual aliasing. This refers to the fact that a purely featural description leaves much ambiguity. For example, the description “door” might fit several places in one’s space. But a door at a particular region is typically a unique description. Having a global frame makes the use of local information unambiguous. It saves the system from having to encode detailed local information.
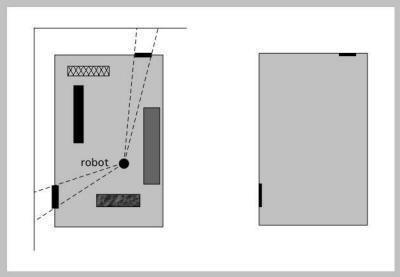 |
| Figure H-2:
Yeap & Jefferies, 1999
|
Another representation that encodes geometry is the Absolute Space Representation (Yeap & Jefferies, 1999). Yeap and Jefferies were concerned with early cognitive mapping, which has the goal of getting a robot to build up a map of the environment it is navigating through. They suggest the strategy of having the robot build an early map of a local environment specifying where boundaries (such as walls) and exits are. The idea is that the robot should at first ‘look past’ furniture that clutter a room (indicated in the left panel by variously shaded rectangles) and figure out where the outer boundaries are. Such a frame with exits allows the robot to navigate through its environment while it builds up more knowledge.
Robotics can benefit the study of animal behavior as well as vice versa (Webb, 2000). The Absolute Space Representation points out the importance of encoding exits. In the animal literature on geometry, the importance of exits has not yet been tested. If exits are important, then they might serve to disambiguate rotational symmetry, whereas other objects of equivalent size might not. Testing this hypothesis is straight forward, and deserves to be done.
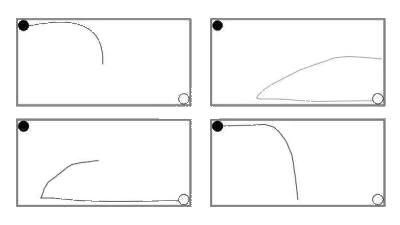 |
| Figure H-
Nolfi, 2002
|
Nolfi (2002) ‘designed’ reactive agents for solving Cheng’s (1986) task up to rotational ambiguity. A reactive agent has no internal states, and reacts to a stimulus always in the same way. “Design” is in quotes because Nolfi actually let the systems evolve. Better solutions got to ‘reproduce’, with some variations, until a system evolved that can readily solve the task. The left panels illustrate a solution for solving the problem starting from the middle, facing one of the walls. Basically, the robot walks with a veer to the left, until it meets a wall. Then it turns left and hugs the wall until it runs into a corner. If the veer is within a certain range, the robot mostly reaches either the correct corner (filled dot) or its diagonal opposite (open dot). The right panels show a similar solution with the middle of one of the sides (facing center) as starting points. Historically, these were the positions used in Cheng (1986).
Nolfi was not concerned to show that animals solve the problem this way. Rather, he was demonstrating the powers of reactive agents.
|