Geometry, features, and orientation in vertebrate
animals: A pictorial review
Ken Cheng and Nora S. Newcombe
Macquarie University & Temple University
Theory of Geometric Encoding
Simpler than shape
 |
| Figure J-1: Principal axes of space |
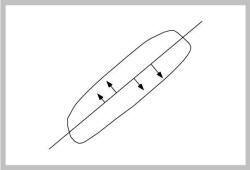
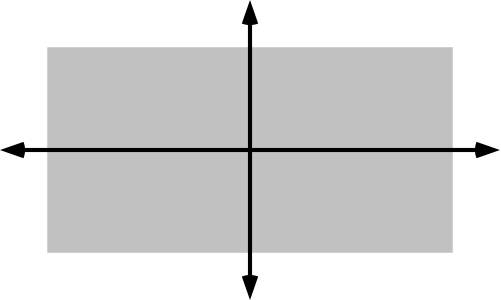
Given the amount of evidence showing that all vertebrate animals tested so far use the geometric properties of space, surprisingly little has addressed how they use geometry or what aspects of geometry play a role. The only prominent theory was formulated by Gallistel (1990, Chapter 6). Gallistel theorized that rats encoded and matched the principal axes of space for determining which direction is which in space. The direction determining is done by matching something far less and far simpler than the entire shape.
The major (long arrow) and minor (short arrow) principal axes of a rectangle are shown here. A principal axis goes through the centroid of the space. A centroid is the center of mass. We have assumed in this diagram that the density of ‘mass’ in the space is uniform, so that the centroid is at the center. But by postulating nonuniform ‘subjective density’ of space, the centroid might be displaced from the center.
The major (first) principal axis has these properties:
-
Mechanically, if the space spins around the axis, it would have the minimum angular momentum.
-
Statistically, the sum of squares of perpendicular distances of points in space to the axis is minimized.
|
|
|
Figure J-2: |
Figure J-2 shows that it is the perpendicular distances to the axis that are minimized, not distances to the principal axis along some arbitrary axis (such as the y-axis, as in statistical regression analyses).
The minor (second) principal axis is perpendicular to the major axis, but we will not be concerned with it.
The principal axis is a computationally shorthand way of coding global directions without having to encode all the details of the overall shape. It is simpler than the geometric module in Cheng (1986) and Egerton et al. (2000), or the Absolute Space Representation of Yeap and Jefferies (1999). It is a parameter that can be matched with a deterministic routine, without the use of iterative trial and error. The matching does not ‘explode’ in complexity as the space becomes more detailed and complicated in shape.
|
|
|
Figure J-3: |
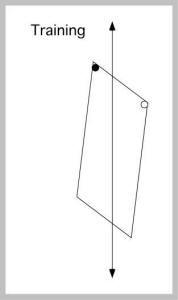
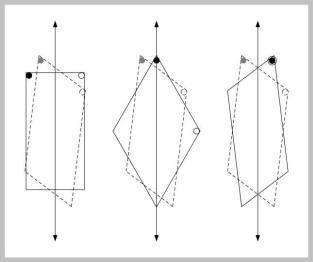
For over a decade, nothing addressed Gallistel’s (1990) theory. Then two papers were published in 2004 that claimed to rule out any global geometric representations, including presumably the theory of principal axes. Pearce, Good, Jones, and McGregor (2004) trained and tested rats in a swimming pool task, with the target escape location at a corner (left). The pool was ringed by curtains and rotated from trial to trial. With no featural cues, the rats of course made rotational errors, as often as correct choices.
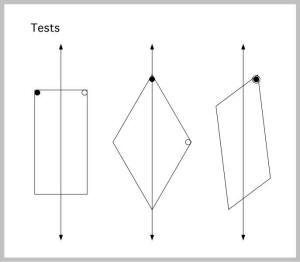
In a crucial test, the shape of the pool was changed to a kite shape (right). This changes Euclidean properties, so that the global shapes of the training and test spaces could not be matched.
The open circles on the right panel show the dominant choices of the rats. The authors thus ruled out matching by shape congruence, although they claimed to rule out all global matching schemes. They favored an explanation in terms of a motor routine (akin to Nolfi’s, 2002, reactive strategy), something like find a long wall and swim to its left end. It is not explained why the rats would not learn to find a short wall and swim to its right end; this would produce searching at the top corner, something the rats hardly ever did.
|
|
|
|
Figure J-4: The rectangle (left) and kite (right) pools used in the Pearce, et al. (2004) experiments. Both pools would be filled with water during experimentation. Thanks to Anthony McGregor for these photos. |
|
|
|
|
Figure J-5: |
Can a formulation in terms of the principal axis of space explain this behavior?
The answer is a definite yes (Cheng & Gallistel, 2005). In Figure J-5, the first principal axis of the test space is shown. In dotted lines, the training situation is superimposed, lined up at middle of the principal axis, and in the direction of the principal axis. Instantly, we see that the rats’ chosen corners are near the ones defined in the training space. One needs to define distance (nearness) properly to favor the top right corner of the kite over the obtuse angle at the top. This is readily done by assuming that the rat is looking for something like: the end of the principal axis and as far to the right as possible.
|
|
|
Figure J-6: |
In this scheme, searching at the apex is akin to a rotational error. When the rat heads down toward the apex end of the kite, it has only one corner to go to.
|
|
|
Figure J-7: |
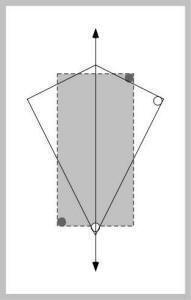
Another study on chicks in an appetitive food finding task had the birds searching for food in one of four containers placed in the corners of a parallelogram. (Tommasi & Polli, 2004). The filled and open dots in the figure above show the target locations of two different groups of chicks. It is crucial to show the results of both locations because they produced important differences.
In the training situation, the chicks, without any featural cues, of course made rotational errors and chose the diagonal opposite to the target as often as the target. In the figures here, this fact is not shown.
|
|
|
Figure J-8: |
Figure J-8 above shows where the chicks searched in transformed spaces. Again, the chicks make rotational errors (not illustrated). They searched at levels as high as in the training space.
The rectangle (left) preserved the lengths of walls, but altered the angles of corners. The authors’ interpretation is that the chicks encoded the relative lengths of walls.
The rhombus (middle) preserved the angles at the corners, but altered the lengths of walls and their ratios to one another. The authors’ interpretation is that the chicks encoded the corner angle.
A reflection of the training space (right) produced the most interesting results. In this space, corner angle and relative lengths of walls were put in conflict. Where the corner angle matched the training situation, the relative lengths were incorrect. For example, for the black-dot group, trained at an acute angle, the long wall was to the right of the short wall in the test space, but to the left of the short wall in the training space. Thus, the acute-angle group (black dots) matched corner angle. The obtuse-angle group (open circle), who chose the same acute-angled corners, matched the relative lengths of walls rather than corner angle. The authors’ interpretation is that an acute angle was more salient than an obtuse angle. The chicks were basically matching on the most salient cue.
|
|
|
Figure J-9: |
Again, can the pattern of results be explained by reference to the principal axis of space, something that the authors rejected?
Again, the answer is a definite yes (Cheng & Gallistel, in press). In this figure, the ghost of the training space (in dashed lines) is again superimposed on each of the test spaces, with the target locations shown in gray for the acute-angle group (black dots in the test spaces), and in open circles for the obtuse angle group (open circles in the test spaces). Again, test spaces and training space are lined up at the principal axis. If the chicks extracted the principal axis of space, and searched at the nearest location according to the training situation, the figure shows that they would search at the observed places that they chose in the test situations. In this case, other than going to a food bowl, there is no need to encode any other local features, such as the angle of a corner.
|
|
|
Figure J-10: |
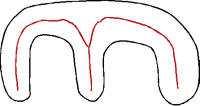
Cheng (2005) suggests that principal axes may not be the best scheme for capturing global shape information. The trouble is that a principal axis is always a straight line, no matter what the shape; it really does not tell us anything about the shape. The M-shape in Figure K-10 has a roughly horizontal straight line as a principal axis, just as a horizontally oriented rectangle would.
In Figure K-10, we have also drawn in red, by free hand and approximately, a set of axes of symmetry. These bend with the curvature of the shape and capture regional symmetries, roughly bisecting the nearest walls. A glance at the red axes shows that they capture the M of the shape. Such axes of symmetry, a variety of them, can be formally defined (see Leyton, 1992, ch. 6).
Another shape-capturing scheme is the medial axis scheme (Fritsch, Pizer, Morse, Eberly, & Liu, 1994; Pizer, Fritsch, Yushkevich, Johnson, & Chaney, 1999), designed for the purpose of medical imaging. In brief this kind of scheme draws a stick-figure trunk and branch structure to capture the gist of the shape. The trunk goes through the middle of the space, and the branches indicate distances to the boundary. Substructures, such as the middle finger of the M in Figure K-10 would have their own skeletons, and be linked to the ‘parent’ shape. The scheme thus also captures something of the structure of the shape.
|
|
|
Figure J-11: |
A priori, it is likely that some kind of global representation of space is used for navigation. The global representation helps the animal to use the right local cues. The problem with local cues is that there are too many of them (the problem of perceptual aliasing, see section on artificial intelligence). The world has too many trees and stones.
Having a sketchy global representation (such as representing key axes) helps the animal limit the amount of local information that has to be encoded. As an example, imagine encoding enough information about a tree shown in this picture to distinguish it from every other tree in this part of a park. The problem taxes the best ‘featural’ systems, and explodes in complexity with the number of trees. If, however, a global representation limits the search to a small region, then the number of trees are limited, and the problem does not explode in complexity. Judiciously combining global and local information might make the task tractable at many scales.
These studies are important in forging ahead with methods for testing theories; they provide good methodological models. Far more research using many transformations is needed to constrain theories of geometric encoding.
|