|
|

|
In the last
two decades there has been renewed interest in animals’ abilities to abstract
information about number and quantity. Number refers to "how many" discrete
things or events are perceived. Quantity is a more general term for amount
and may involve an assessment of number or of other dimensions. The broader
question underlying this research is how animals, that are by definition
non-verbal organisms, can encode information about number or quantity when
they are presented with stimuli that are variable in other respects. Often
they also have to retain this abstracted information at least long enough
to be able to use it as a basis for making behavioral decisions. The question
of animals’ cognitive abilities is interesting in its own right. But some
of the research to be described in this chapter may also give insights
into the abilities of pre-verbal infants to process number or quantity,
or indeed into the adult capability of assessing these abstract dimensions
without having to enumerate or measure the things they perceive.
This chapter looks mainly
at how birds perform on a variety of number-related tasks in which visual
stimuli have been used. Some of the pioneering studies that were done on
this topic have often been overlooked. They provide an important foundation
for more recent research and will be reviewed briefly. Then newer research
is discussed which has examined how birds judge relative differences in
the numbers of items they see. Besides making relative judgments, some
birds can assess absolute amounts within the small number range. Birds
can also discriminate relative differences in proportion when the stimulus
quantities are either continuous areas of color or are mixtures of numerous
colored items. Various models have proposed how non-verbal organisms might
process such an abstract property as number. This chapter also considers
ways in which the ability to assess the number of things birds encounter
in their general environment may be advantageous to them in an evolutionary
sense.

|
I.
Delving into History
Anecdotal
Beginnings
For at least two hundred
years, people have speculated about whether animals can in some sense "count",
or make choices based on number. This possibility was first raised in a
popular anecdote about crows. The story goes that whenever a hunter tried
to approach a crow and shoot it, the bird kept its distance. So the man
enlisted the help of others in a ruse that was designed to trick the bird
into deciding it was safe to return to its nest. A group of hunters entered
a hiding place in sight of the bird, then after a while all but one left
again, leaving the last person concealed. When there were up to 5 people
in the group, the crow stayed out of harm’s way until the remaining hunter
had also given up and left. The bird was fooled into returning prematurely,
and met its demise, only when there was a total of 6 hunters. No doubt
this story is apocryphal, but it points to two ideas. The first is that
birds can accurately keep track of the number of things (such as hunters
in a group) up to some limit (in this example 5 but not 6); the second
is that being able to do so might have survival value, and so be of evolutionary
significance.
The
Need for Controls
The earliest attempts to
find experimental evidence of numerical abilities in birds (and in other
animals) were not very successful though. For instance, in an experiment
with house-sparrows, Porter (1904) tested their response to number by hiding
food under, say, the third container in a row, then recording which container
a bird flew to first on repeated trials. Then he changed the number of
the baited pot and tested the birds’ ability to redirect their choices.
After extensive testing, Porter concluded that the sparrows based their
choices mainly on the location of the food container -- the relative distance
of the baited one from the end of the row, rather than its numerical order
within the row. Although this early work failed to provide evidence for
a response to number, it pointed to the importance of the conditions for
testing an animal’s potential numerical abilities, and the need for controls.
In Porter’s study, there were at least two procedural defects. As Porter
himself recognized, the serial number of the baited container was confounded
with a relative distance measure, since the containers were placed equidistant
from each other in all the tests. Also, the birds were always allowed to
take a bit of food, whether the correct container was chosen or not. So
in modern parlance, the birds were non-differentially reinforced. Apparently,
Porter tried to "make them do without" food when they chose the wrong container,
but this made their behavior even more erratic.
The other early lessons about
the importance of controlled procedures stem from work that was done with
a horse, nicknamed Clever Hans. Its owner, von Osten, trained the animal
to perform a variety of feats, including responding to numbers that were
written on a chalkboard, and performing arithmetic calculations. The horse
responded by tapping its hoof on the ground the correct number of times.
Initial investigations of its behavior convinced a panel of scientists
that the animal could indeed answer questions that involved counting, apparently
without its owner’s intervention. However, one scientist, Pfungst, eventually
discovered that the horse answered correctly only when its owner knew the
answer, and when it could see its owner while it responded. Clever Hans
was actually able to detect minute changes in von Osten’s behavior that
he made unwittingly when the horse reached the correct count with its hoof-tapping
(see Candland, 1993, for a full account). Although von Osten had not intended
to deceive others about his horse’s abilities, most studies since then
have tried to preclude the possibility of cueing an animal to give the
correct response. One way of doing this is to test animals in a setting
in which interactions with the experimenter are minimized. This is more
easily achieved now than was possible at the beginning of the last century.
Many of the more recent experiments use standardized procedures with the
animals in training chambers in which stimuli are presented, and the animals’
responses are recorded with the help of computers.
Ethological
Experimentation
Although there were several
other early studies on animals’ numerical abilities (see Thorpe, 1963;
Rilling, 1993), the first real progress was made in this field by Otto
Koehler and his collaborators. Their experiments were performed in quasi-naturalistic
settings on a variety of animals, including several avian species – pigeons,
jackdaws, a raven, an African Grey parrot, and budgerigars (see Koehler,
1941). Koehler concluded that birds have two basic numerical abilities.
One, based on a visuo-spatial sense, enables them to assess the number
of items presented simultaneously in a group, while the other allows them
to assess the number of events that occur successively, or spread out in
time. Koehler devised various training procedures to investigate these
abilities.
Pigeons were trained, for
instance, to approach a strip of cardboard on which there were two sets
of grain that differed in number. A bird had to choose the set containing
a particular amount (e.g., 4 grains) and was allowed to eat this set as
a reward. (See Figure
1 for a reconstruction of this type of choice.) To prevent it eating the other set (of say 3 grains), Koehler shooed the
bird away if it reached toward the incorrect group. At different stages
of training, the correct set sometimes contained the larger and sometimes
the smaller number of grains. Every effort was made to avoid cueing of
the type that Clever Hans had utilized. The experimenter hid behind a screen,
out of sight of the bird. The punishment of shooing a bird away was delivered
in a standardized fashion by a mechanical device. Punishment for incorrect
choices was withheld on some test trials. Also, the reactions of the birds
were filmed to provide an objective record of their behavior.
To prevent it eating the other set (of say 3 grains), Koehler shooed the
bird away if it reached toward the incorrect group. At different stages
of training, the correct set sometimes contained the larger and sometimes
the smaller number of grains. Every effort was made to avoid cueing of
the type that Clever Hans had utilized. The experimenter hid behind a screen,
out of sight of the bird. The punishment of shooing a bird away was delivered
in a standardized fashion by a mechanical device. Punishment for incorrect
choices was withheld on some test trials. Also, the reactions of the birds
were filmed to provide an objective record of their behavior.
One jackdaw in particular
was successful in a matching to sample task. After looking at an array
of blobs on a "sample" card, the bird had to remove the lid from one of
two pots in order to find a hidden food reward. On each lid were other
arrays. A correct choice, which led to reward, was to remove the lid with
the same number of marks as on the sample card. An incorrect (and thus
unrewarded) choice was to remove the lid in which the number of marks differed
from the sample number. The bird that performed best on this task could
match the numbers of items on the sample card and the comparison lid even
when the configuration of blobs and their sizes differed (both between
and within trials), so that the only common feature was their number. Another
jackdaw was correct in its matching behavior when the patterns of the blobs
differed between the card and the numerically matching lid, but its choices
were not statistically reliable when the blob sizes varied. In this case,
as Koehler recognized, the bird’s performance did not guarantee that it
was discriminating solely on the basis of equality of number. Instead,
it could have been comparing the overall areas of the stimulus marks on
the card with those on the lids.
Other studies looked at birds’
ability to "act on number", as Koehler put it, i.e. to respond sequentially
until a specific number of items had been obtained or events had been completed.
For instance, pigeons and budgerigars were trained to eat only a given
number of seeds from a much larger number they saw. So if they were required
to take exactly 4 seeds their behavior was scored as correct if they walked
away after eating the fourth food item, but they were automatically shooed
away if they tried to eat a fifth item. The accuracy of their performance
was tested on trials in which this mild punishment was withheld. In another
experiment with pigeons, peas were delivered one at a time down a chute
into a large dish. In this experiment, the time interval between deliveries
was randomly varied to prevent the birds estimating the total time that
had expired, rather than the number of items taken. Koehler also argued
that it was the number of peas, rather than the number of pecks, or the
pecking rhythm, that was important since the pigeons often had to peck
several times at a rolling pea before they could grasp it.
With jackdaws, the task consisted
of taking the lids off pots until a specific number of hidden food items
had been retrieved, after which the remaining pots in the row would be
empty. The important feature of this experiment was that on successive
trials, the same number of food items was differently distributed. Suppose
that the number of food items available was 2, but their distribution varied
across trials. The bird had to open just one pot if both items were in
the first pot, 5 pots if there was one piece of food in the first and in
the fifth pots, 2 pots if 1 item was hidden in each of the first two pots
in the row, etc.
From these and other studies,
Koehler concluded that birds have at least a limited ability to discriminate
objects or events on the basis of their numerosity and inferred that animals
have some way of internally tagging the items they have seen or responded
to. Koehler was careful to say that animals do not seem to count in the
way that an adult human might by precisely enumerating items with a fixed
series of symbolic labels (e.g. one, two, three, four, or eins, zwei, drei, vier, etc., depending on linguistic culture). Rather, he argued that animals
learn what he called "unnamed numbers", so that four items might be represented
by a series of inner marks or tags. He also noted that different species
showed remarkable similarities in the limits of their ability to discriminate
numerosity. Mostly the accuracy of their performance broke down when the
number of items or events they had to respond to was between 5 and 6, or
6 and 7 (Koehler, 1943).
Developments
Post-Koehler
Despite his efforts to eliminate
extraneous cues, Koehler’s work has still been criticized for lack of control.
Wesley (1961) pointed out, for instance, that there was little control
for olfactory cues in the experiments involving hidden food, and that seeds
were arranged by hand on cards, which could have led to some subjective
bias. In spite of these remaining criticisms, subsequent experiments have
done more to corroborate than to refute Koehler’s basic findings. As one
example (Knorn, 1987; see Emmerton & Delius, 1993), 8 pigeons were trained using
standard operant techniques to discriminate between simultaneously presented
arrays of white dots upon the dark background of two pecking keys. All
the events in the training chamber (presenting the stimuli, recording the
birds’ pecks, giving them a food reward, etc.) were controlled by a computer.
The number and the size of dots in the arrays varied across training trials,
but pecks at the array containing the greater number of dots always led
to food reward whereas pecks to the less numerous array led to timeout
(a short period of darkness). After they had reached a fairly stable level
of choosing the greater numerosity on training trials, transfer trials
with novel stimulus arrays were later added. Some of these novel test stimuli
are shown in Figure 2.
As an
additional control for brightness differences, luminance was equated in
each pair of test arrays. Finally, neither food reward nor timeout reached a fairly stable level
of choosing the greater numerosity on training trials, transfer trials
with novel stimulus arrays were later added. Some of these novel test stimuli
are shown in Figure 2.
As an
additional control for brightness differences, luminance was equated in
each pair of test arrays. Finally, neither food reward nor timeout 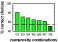 was given on the transfer trials. When the test data for various numerical
combinations were averaged across birds and test sessions, the results
resembled those found by Koehler. In this case, the pigeons could still
discriminate arrays of 6 vs. 7 dots at an above chance level, but performance
dropped to chance on test trials in which 7 vs. 8 dots were shown (see
Figure
3).
was given on the transfer trials. When the test data for various numerical
combinations were averaged across birds and test sessions, the results
resembled those found by Koehler. In this case, the pigeons could still
discriminate arrays of 6 vs. 7 dots at an above chance level, but performance
dropped to chance on test trials in which 7 vs. 8 dots were shown (see
Figure
3).
This experiment confirms Koehler’s findings when there is a difference
of one item between paired stimulus displays. However, more recent research,
described later in this chapter, has shown that the question of the limits
of discrimination has wider implications than was previously supposed.
Koehler’s work provided an innovative foundation for subsequent research
into animals’ numerical abilities. He and his colleagues devised a remarkable
variety of procedures for training and testing a wide range of species.
The published reports of these experiments also contain a wealth of detailed
observations about the animals’ behavior during the experiments. Since
the '30’s and '40’s when most of Koehler’s work was done, there has been
renewed interest and considerable progress in investigating how animals
discriminate things in terms of their number. Some of this work has been
reviewed in articles by Davis and Memmott (1982), by Davis and Pérusse
(1988), and in a book edited by Boysen and Capaldi (1993). Further research
has been completed since those reviews appeared.
II.
Number as an Abstract Property
Number represents one of
the abstract properties of items or events in the environment, or of actions
that organisms can perform. When we refer to number we mean that this aspect
of quantity – "how many" discrete elements -- remains the same even when
other characteristics change. For instance, "five" might be our verbal
label to describe a group of large oranges, a line of small pebbles, a
series of whistles, or how many times we knock on a door. Animals presumably
also have a way of internally representing (or encoding and remembering)
these different amounts. However, as Koehler pointed out, animals obviously
rely on non-verbal coding mechanisms to discriminate and store information
about number. Only a few studies have shown that animals can learn symbols,
similar to our digits, to represent the number of things, but they do this
only after prolonged training.
Davis and Pérusse
(1988) have discussed in detail the different types of competence that
animals may show in numerical discrimination tasks.
Most of the experiments described in this chapter correspond to two types
of numerical competence. Birds have been tested mainly for their ability
to discriminate numerosity. Numerosity discrimination requires only relative
or ordinal judgments. For instance, a bird must show that it perceives
one stimulus as having "more" items compared with another that has "less",
or one consists of "many" elements while another has "few". However, with
these relative judgments the animal does not necessarily have to recognize
the precise number of elements in a stimulus. To demonstrate proper counting
ability, several criteria must be met (Gelman & Gallistel, 1978). These
include tagging items one by one, irrespective of their type, so that the
final tag represents the precise or cardinal number of items in a stimulus.
Essentially, the animal must be able to recognize that a stimulus consists
of exactly three elements, for example. Some birds have learned to respond
to small numbers of elements quite accurately. An African Grey parrot has
learned to "speak" the correct number (Pepperberg, 1987). Pigeons have
been trained to emit specific numbers of pecks when shown one of several
digit-like symbols (Xia, Siemann & Delius, 2000). These studies will
be described later (see section IV on cardinal numbers and counting).
III.
Relative Judgments and Numerosity
When animals are tested for
their ability to make numerosity judgments, they are presented with the
task of deciding whether 5 items are more than 3, or whether there is a
greater number of sound pulses in a series of 8 versus 4 tones.  Although the experimenter devises stimuli with knowledge of the exact numbers
of items, this does not mean that the animal has to know anything about
the precise numbers in order to make a correct choice. To get an idea of
why this should be so, look at Figure
4. Without
having to enumerate each grain, it is still possible to say that there
are more seeds in one patch than in another.
Although the experimenter devises stimuli with knowledge of the exact numbers
of items, this does not mean that the animal has to know anything about
the precise numbers in order to make a correct choice. To get an idea of
why this should be so, look at Figure
4. Without
having to enumerate each grain, it is still possible to say that there
are more seeds in one patch than in another.
Experiments on numerosity
discrimination examine, on the one hand, how birds judge the relative numbers
of items that are presented simultaneously in visual arrays, and, on the
other hand, how they judge differences in the numbers of items shown sequentially.
Discrimination
of Visual Arrays
Visual arrays were used by
Honig to test pigeons with a go/no-go procedure. In the initial experiments
(Honig & Stewart, 1989), the birds were trained that food reward would
follow when they pecked a key on which they saw a uniform array of "positive"
colored dots (e.g. red) for 20 sec. If an array with the same number of
dots but all in a "negative" color (e.g. blue) appeared for the same 20
sec, pecks were not rewarded. Once they had learned to respond to the positive
array but not to the negative one, they were tested in extinction (without
reward) with various arrays in which the total number of dots stayed constant,
but the relative numbers of red to blue ones varied. The relative amount
of pecking to these arrays diminished as the proportion of positive-colored
dots in the array decreased from 100% to 50%. By itself, this does not
prove that the pigeons could discriminate numerosity since they might instead
have responded to a particular summed area of, say, the red color. But
other tests did show that they were relying on the relative number of different
types of items in the arrays. Changing the total number of dots per array
did not alter their discrimination performance. In other tests the dots
differed in size rather than color so that the birds had to discriminate
how many large versus small dots there were. The stimuli were devised so
that a simple discrimination of area was unlikely. In other parts of the
experiment, black and white shapes (Xs and Os) were used instead of colored
dots. Finally, tests were conducted with arrays made up of complex and
rather variable shapes that fell into two categories – stylized pictures
of birds versus flowers. In spite of this variability in the color, size
or form of the items in the arrays, the pigeons’ amount of responding changed
with the relative numbers of items within a given array.
With similar procedures Honig
and Stewart (1993) have shown that pigeons respond to the "abstract" dimension
of numerosity in ways that resemble their reactions to the "perceptual"
dimensions of much simpler stimuli. An example of this is the "peak shift"
effect which is shown when there is more responding to a test value than
to the rewarded value of the positive or S+ training stimulus. The direction
of this shift is away from the negative or S- value. It is seen with dimensions
such as hue (or spectral wavelength) or stimulus size, and it shows that
animals often assess relative differences amongst stimulus values. Honig
and Stewart also demonstrated the peak shift when pigeons were trained
to peck arrays consisting of equal numbers of two types of elements (e.g.
red and blue dots), and not to respond when the arrays consisted of relatively
more of the negative color (e.g. more blue than red dots). The birds were
then tested with arrays in which the relative numbers of dots in the two
colors varied. In these tests they responded more to arrays containing
a greater proportion of positive elements (e.g. red dots) than they did
to the originally rewarded S+ array with its equal numbers of red to blue
items. This peak shift effect still occurred when the total number of dots
in the test arrays was increased (while the proportions of red to blue
were maintained). The effect was also seen when arrays consisted of horizontal
and vertical rectangles rather than colored elements. So once more, the
important dimension was the relative number of items. Honig and Stewart
gave examples of how the peak shift phenomenon might be of functional significance
for birds, and other animals. If a bird has to select amongst food patches
where berries are ripening, they can learn that it is better to choose
the patch in which half the berries are ripe, rather than one in which
only a small proportion has ripened. But it is better still to find a patch
in which more than half the berries are already ripe.
Instead of testing pigeons
with a go/no-go procedure, Emmerton, Lohmann and Niemann (1997) used a
conditional discrimination procedure. First, a bird had to peck at a visual
array that was shown on a center key. If the array contained "many" items
(6 or 7) then the pigeon had to peck at one of the side keys (e.g. the
right-hand red-lit one) to obtain a food reward. If instead the center
array contained "few" items (1 or 2) then the correct response was to choose the other side key
(e.g. the left-hand green-lit one). Incorrect choices led to a timeout
period of waiting several seconds in the dark. (Click here for animated
illustration.) A variety of these arrays containing 1, 2, 6 or
7 items were shown until the birds had learned to discriminate accurately
between "many" and "few" items. Then they were tested not only with new
versions of the "many" and "few" stimuli, but also with arrays consisting
of the intermediate numbers 3, 4 and 5. These numbers were completely novel
for them. Also, on test trials there was
items (1 or 2) then the correct response was to choose the other side key
(e.g. the left-hand green-lit one). Incorrect choices led to a timeout
period of waiting several seconds in the dark. (Click here for animated
illustration.) A variety of these arrays containing 1, 2, 6 or
7 items were shown until the birds had learned to discriminate accurately
between "many" and "few" items. Then they were tested not only with new
versions of the "many" and "few" stimuli, but also with arrays consisting
of the intermediate numbers 3, 4 and 5. These numbers were completely novel
for them. Also, on test trials there was 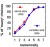 no reward or timeout and so no feedback about correct or incorrect choices.
The test choices were plotted as the percentage of choices made to the
side key that denoted "many" (see Figure
5). Most of the "many" choices were made when the center test-array
contained 6 or 7 elements, and the least choices when the array consisted
of 1 or 2 items. In this respect the birds treated these novel arrays as
they had the familiar training stimuli. When the intermediate numbers were
shown, the birds’ choices were distributed in an orderly fashion. Compared
to their responses with arrays of 6 or 7 items, they made slightly fewer
choices of the "many" key when the test-array contained 5 items, fewer
when it had 4 items in it, and fewer still when there were 3 items. This
distribution of choices indicates that pigeons can serially order numerical
quantities so that 7/6 > 5 > 4 > 3 > 2/1.
no reward or timeout and so no feedback about correct or incorrect choices.
The test choices were plotted as the percentage of choices made to the
side key that denoted "many" (see Figure
5). Most of the "many" choices were made when the center test-array
contained 6 or 7 elements, and the least choices when the array consisted
of 1 or 2 items. In this respect the birds treated these novel arrays as
they had the familiar training stimuli. When the intermediate numbers were
shown, the birds’ choices were distributed in an orderly fashion. Compared
to their responses with arrays of 6 or 7 items, they made slightly fewer
choices of the "many" key when the test-array contained 5 items, fewer
when it had 4 items in it, and fewer still when there were 3 items. This
distribution of choices indicates that pigeons can serially order numerical
quantities so that 7/6 > 5 > 4 > 3 > 2/1.
Several tests were conducted
in this experiment to make sure that the birds really discriminated the
numbers of items in the arrays, rather than detecting some other confounds.
To begin with, all the items in a given array were the same size and shape
(e.g. all white dots on a dark background). Although item sizes differed
between arrays, it was likely that, as the number of items changed, so
on average did the summed area of these elements, as well as their overall
brightness. So in other tests, the brightness was equated across stimuli
with filters, or the total area of the dots was held equal by altering
their sizes. This did not change the birds’ performance with the various
test numerosities. In further tests, shapes other than dots were used, dots of mixed sizes were presented, or the arrays
consisted of mixtures of outline and filled-in shapes (to mimic mixtures
of light and dark seeds). (See Figure
6 for examples of various test arrays.) In these and other tests,
none of the alterations to the specific stimulus characteristics had any
consistent effect on the birds’ distributions of choices to the "many"
and "few" side-keys. In all the tests, they behaved as if they were responding
in an orderly way to the number of items they saw. In spite of this pattern
of behavior, the experiment still does not show that the birds recognized
there were exactly 3 or else 6 items in an array. Although the distribution
of choices was orderly, it was not exactly linear. Instead, it seemed to
be easier for the birds to discriminate amongst the smaller numbers (1
to 4) than amongst slightly larger numbers (5 to 6). This non-linearity
gives some clues about the processing of relative number, as will be discussed
later.
than dots were used, dots of mixed sizes were presented, or the arrays
consisted of mixtures of outline and filled-in shapes (to mimic mixtures
of light and dark seeds). (See Figure
6 for examples of various test arrays.) In these and other tests,
none of the alterations to the specific stimulus characteristics had any
consistent effect on the birds’ distributions of choices to the "many"
and "few" side-keys. In all the tests, they behaved as if they were responding
in an orderly way to the number of items they saw. In spite of this pattern
of behavior, the experiment still does not show that the birds recognized
there were exactly 3 or else 6 items in an array. Although the distribution
of choices was orderly, it was not exactly linear. Instead, it seemed to
be easier for the birds to discriminate amongst the smaller numbers (1
to 4) than amongst slightly larger numbers (5 to 6). This non-linearity
gives some clues about the processing of relative number, as will be discussed
later.
A parameter that was not
systematically altered in the last experiment was the density of the arrays,
or the spacing between the dots. The effect of changes in density was examined
separately (Emmerton, 1998). This time, pigeons were trained to discriminate
pairs of arrays that were shown simultaneously on two pecking keys. The
birds’ task was to choose the array with fewer dots in it in order to obtain
reward. Different combinations of small numbers of dots were used. Mostly,
the birds were more accurate at choosing the smaller numerosity when the
difference between the S+ (smaller-number array) and the S- (larger-number
array) was greater rather than smaller. For instance, the birds were better
at discriminating 3 from 7 dots than they were 3 from 5 dots. But in addition
to the relative difference in numerosity, the inter-dot spacing in the
various arrays affected the accuracy of the pigeons’ discrimination. In
some training sessions, the correct, S+ array consisted of only 1 dot,
and the incorrect, S- array contained either 2 or 3 dots. Discrimination
performance was better when the S- array had closely spaced dots than when
they were far apart. When both arrays in a pair contained multiple dots there were four combinations of high density ("near" spacing) and low density
("far" spacing) for each numerosity pair. In different series of training
sessions, the stimulus pairs consisted of 2 vs. 3 or 4 dots, 3 vs. 5 or
7, or else 5 vs. 6 or 7. (See Figure
7 for examples of the stimuli.) In each case, the best discrimination
scores on average were obtained when the small numerosity, S+ array had
widely spaced dots and the larger numerosity, S- array had closely spaced
dots. The poorest performance was obtained with the opposite density combinations,
i.e. "near" spaced S+ array vs. "far" spaced S- array. These rankings of
performance level are summarized in Table 1.
there were four combinations of high density ("near" spacing) and low density
("far" spacing) for each numerosity pair. In different series of training
sessions, the stimulus pairs consisted of 2 vs. 3 or 4 dots, 3 vs. 5 or
7, or else 5 vs. 6 or 7. (See Figure
7 for examples of the stimuli.) In each case, the best discrimination
scores on average were obtained when the small numerosity, S+ array had
widely spaced dots and the larger numerosity, S- array had closely spaced
dots. The poorest performance was obtained with the opposite density combinations,
i.e. "near" spaced S+ array vs. "far" spaced S- array. These rankings of
performance level are summarized in Table 1.
|
Table 1. Array density and discriminablity
of numerosity
|
|
Numerosity Combinations
1/2 - 1/3
2/3 - 2/4
3/5 - 3/7
5/6 - 5/7
|
Performance rankings
N-> F-
F+N-
> N+N- > F+F- > N+F-
F+N-
> F+F- > N+N- > N+F-
F+N-
> N+N- > F+F- > N+F-
|
Array size:
+ = smaller number
Dot spacing: F = "far" = low density
- = larger number N = "near" = high density
|
The explanation of these effects
of stimulus density may be that the birds "scan" each array. They were
always meant to choose the stimulus with fewer items in it. Suppose that
a bird looked at the S- array with more dots in it, but these were spaced
out. If it did not completely scan the whole pecking key, there was a greater
probability that it missed one or more dots than if the dots were all close
together. So with a low density S- there was a greater likelihood that
a bird would falsely choose that stimulus, as if it actually contained
fewer dots. The pigeon would be less likely to overlook an item if the
dots were close together, so this type of ‘false alarm’ error was less
likely to occur with a high density S- array. The basic suggestion here
is that birds scan across multi-item stimuli, processing items one after
the other. If this is the case, then the way they deal with "simultaneous"
arrays is essentially to process the items in them sequentially. This would
provide an important link to the other types of experiments that have been
done to investigate birds’ ability to differentiate numbers of items.
Discrimination
of Sequential Stimuli
In these other studies, birds’
numerosity judgments have been tested with sequences of visual stimuli,
rather than with spatial arrays. Although Koehler’s earlier work demonstrated
that pigeons can learn to keep track of a given number of pea-seeds, presented
to them one by one down a chute, there was no precise control over temporal
parameters. Time factors were certainly varied, both intentionally by rolling
the peas down the chute at slightly irregular intervals, and unintentionally
due to the birds’ occasional difficulty in grasping a moving pea. More
recent experiments on pigeons have used sequences of light flashes as the
stimuli. With these stimuli, the duration of a light flash as well as the
timing of the intervals between successive flashes can be controlled with
much greater precision.
Alsop and Honig’s (1991)
approach was to flash a series of colored lights onto a center key that
pigeons had to peck. If there were more red than blue flashes in a series,
then choice of one side key was correct. If instead blue flashes were in
the majority, the correct response was to choose the other side key. The
birds were tested with up to 9 flashes in a series but it was the relative
rather than the absolute number of light flashes in one versus the other
color that was important in determining which side key the birds chose.
Alsop and Honig also discovered that later flashes in a sequence had more
influence on the birds’ choices than did light stimuli that were near the
beginning of a series. So in a mixed sequence of red-blue-blue-blue-blue
lights, the birds were more likely to peck the side key indicating that
there were more blue flashes than if the sequence was blue-blue-blue-blue-red.
The experimenters varied either the total number of light flashes in a
sequence or the duration of the dark-interval between flashes. This revealed
that not only the ordinal position of a flash in a sequence affected the
accuracy of a bird’s choices but also the time that went by between its
seeing a flash of a particular color and having to peck a side key. The
pigeons showed a "recency" effect in their memory for which flashes had
occurred in the sequence. The duration of each light flash also had an
effect on their accuracy. Extending the duration of each light flash probably
made it more salient so that the birds’ performance was slightly better
when flashes were longer than when they were shorter. This experiment showed
that, although birds can discriminate the relative numerosity of items
in a sequence, temporal factors influence their memory for how many items
they have seen.
A recent experiment by Keen
and Machado (1999) has also looked at the way pigeons discriminate the
relative frequencies (or numerosities) of two series of events – a sequence
of red lights shown on one key versus a series of green lights on another
key. In this experiment (unlike Alsop and Honig’s), lights of the same
color were always shown consecutively. Which series (red or green, and
larger or smaller number) appeared first or last was counterbalanced across
trials. After the stimulus sequences, two keys were lit red and green.
The birds had to choose the color that had appeared least frequently. The
total number of stimulus events and the difference in frequencies of red
vs. green lights were systematically varied across trials. Both these parameters
affected the birds’ accuracy in indicating which series included fewer
events. Their key-choices were related to the relative frequencies of red
and green lights -- the bigger the difference in number, the more accurate
their choices, but their discrimination also depended on the total number
of stimuli. The total number (that ranged between 4 and 28) had other effects
on their choices too. The pigeons showed "recency" effects, similar to
those reported by Alsop and Honig (1991), when there were more than 8 colored
lights altogether, but they showed "primacy" effects with fewer stimuli.
A "recency" effect means that the last stimulus series more strongly influenced
the birds’ choices about the relative number of events, whereas a "primacy"
effect means that the first series of stimulus events had more effect on
the animals’ decisions. Although the birds’ choices were related to stimulus
numerosities, Keen and Machado explained their results not in terms of
numerical abstraction by the birds but rather with a mathematical model
based on cumulative stimulus effects and decay functions (see section VI).
Roberts, Macuda and Brodbeck
(1995) found a similar "recency" effect in pigeons’ memory for the number
of light flashes. In their experiment, stimuli always consisted of series
of red-light flashes. Initially, some birds were trained to choose one
color of side-key if there was a small number of flashes (2) in the series
and another color of side-key if there was a larger number (8). The overall
time for the series was held constant at 4 sec. When there were only 2
flashes, one occurred at the start of the 4 sec period and the other at
the end. With 8 flashes, these events were spaced evenly throughout the
4 sec. For other birds, time varied rather than number. Four flashes were
spread out over 8 sec or else over 2 sec. Different side keys had to be
chosen depending on the duration ("long" vs. "short") of the sequence.
In the initial training, choices to the side-keys could be made immediately
after the end of the stimulus sequence (0 delay). But in subsequent tests,
the delay varied between the end of the light-flash series and the opportunity
to choose a side-key.
The result of varying this
delay indicated two things that were confirmed in a subsequent experiment.
Firstly, the birds discriminated the number of events (light flashes),
even when their training had been designed as a time-discrimination task.
Secondly, they appeared to remember more accurately those events that had
occurred in the most recent window of time. When the delay increased, birds
in the number-discrimination group still chose the "small-number" side-key
after 2 events. Given the choice between "small-number" and "large-number"
this would be the appropriate response even if they remembered just the
light flash at the end of the fixed 4 sec stimulus period. But as the delay
increased these birds were more likely to choose the "small-number" rather
than the "large-number" key after 8 flashes. So with longer delays they
remembered only the events towards the end of the stimulus period and reported
fewer events than there had actually been. Pigeons in the time-discrimination
group also behaved differently when delays were introduced. As delays increased,
there was little change in their accurate choice of the key for a "long"
(8 sec) series of flashes. However, following a "short" 2 sec series they
shifted their choices to the key for a "long" series instead. In a "long"
sequence, the light flashes occurred at a low rate, so if the birds only
remembered the events at the end of a stimulus period, they treated this
stimulus sequence as if it contained only a small number of events.
In a "short" stimulus series, there was the same number of events but they
occurred in a briefer time period. At short delays, the birds responded
as if they remembered "many" light flashes. But as delays increased,
they remembered only the most recent stimulus flashes and so responded
as if there were a small number of them. Essentially then
the "long" key meant "small-number" for them and the "short" key meant
"larger-number".
Other experiments (Roberts
& Mitchell, 1994; Roberts & Boisvert, 1998) showed that pigeons
can concurrently process both the time interval and number of events for
series of light flashes. In the first of these experiments (described in
the chapter by Sutton and Roberts, this volume), the stimulus series and
the training procedure were similar to those used by Roberts et al. (1995),
except that no delay interval was imposed between the end of a stimulus
sequence and the opportunity to choose a side-key. In the second experiment,
the stimuli and procedure were slightly different. Roberts and Boisvert
(1998) presented light stimuli on a pecking key. A stimulus series began
when the key turned green. When the key briefly flashed red instead of
green, this was an ‘event’ in the series. In their initial training, time
and number were confounded: the birds’ key-pecking was rewarded when 20
red flashes had occurred so that the stimulus series lasted for 20 sec.
The rate at which red flashes appeared was then manipulated and the birds
were tested using the peak-procedure. On test trials, no food reward was
given but the stimulus series continued for 100 sec so that changes in
pecking rate could be measured. These test trials indicated that either
the number of events or else the time elapsed influenced the birds’ peak
rate of responding, which was indicative of their expectation of a food
reward. But the pigeons could also be trained that reward depended specifically
on the number of events, for some birds, or the duration of a series, for
others. These two experiments suggested that time is a more salient dimension
than number for pigeons, which is slightly different from the conclusion
reached by Roberts et al. (1995). However, the birds’ bias to base their
decisions on time rather than number when either dimension could be used
was easily altered by differential training. The close relation between
timing and counting that these experiments revealed has been used by Roberts
and his colleagues to develop a model to explain how birds process these
two aspects of sequences of events (see section VI).
IV.
Cardinal Numbers and Counting
In the studies described
so far, the birds clearly showed that they could judge relative differences
in the numbers of items, but they were not required to choose stimuli according
to the absolute number of items they contained. Can birds in fact respond
differentially on the basis of absolute number if required to do so? Can
they actually count? Although the term "counting" is often applied loosely
to any behavior that involves numerical discriminations, a number of criteria
have to be met before an animal can really be said to count (Gelman &
Gallistel, 1978;). These criteria include assigning
in a one-to-one way a tag to each item in a set. Tagging might be evident
if an animal responds by pecking, or touching, each item in turn. But a
physical response might not be obvious. More important is the idea that
the animal cognitively keeps track of each item in a set and assigns each
one a code. These codes are called numerons by Gelman and Gallistel (1978).
This is similar to Koehler’s suggestion that an animal uses a series of
‘inner marks’ to represent each item it has seen. The order in which the
various items themselves are tagged is irrelevant. Also the animal should
be able to tag any type of item so that the number in a set is an abstract
quantity that is not tied to any specific characteristics (such as size
or shape) of the items to be counted.
The mental tags, or symbols
that represent each tagged item, must be applied in a particular order.
For instance the tag for 4 things always follows the tag for 3 things which
in turn follows the tag for 2 items. Then, when the final item in the set
is tagged, the mental code or symbol applied to that item is the cardinal
number – the total amount in the set. So counting involves the ability
to judge absolute, or cardinal, numerical amounts or numbers of responses.
The best evidence for counting comes from studies of non-avian species
(e.g. rats: Capaldi & Miller, 1988; chimpanzees: Boysen & Berntson,
1989). Most of the work with birds demonstrates their ability to estimate
relative differences in number rather than to count or judge the absolute
number of things. A notable exception is Pepperberg’s
(1987, 1994) investigations of the abilities of Alex, an African Grey parrot.
Alex had had extensive training to vocalize English words as verbal labels
for different objects, shapes and colors. In addition, he learned to respond
to the verbal question "How many?", spoken by his trainer, with a numerical
label for the quantity of items he was shown. Alex was initially trained
to use numerical labels to describe classes of shapes as "3-corner" or
"4-corner" (Pepperberg, 1983). Then, over a period of several years, intermixed
with training on other tasks, he was gradually taught the labels for between
2 and 6 objects (Pepperberg, 1987). In response to the question "How many?"
he was at first required to vocalize not just the quantity but also the
name for the type of objects. He accurately gave answers like "4 key" (the
use of plurals was not required; To
see a video of Alex performing click here, this video is 58 seconds in
duration, so download times will be longer then most of the videos in this
book). His previous experience with shapes was
extended to items such as "6-corner paper". He also learned to tell the
number of objects in a subset within a heterogeneous array, e.g. when asked
"How many cork?" he could answer "2" when shown a random mixture of 2 corks
and 3 keys. His ability to label cardinal sets accurately transferred to
other objects for which he knew the names but which had not been used in
numerical training. So Alex used "spoken" numbers as abstract labels. Interestingly,
when he was questioned about the number of unfamiliar objects in mixed
arrays of known and novel items, his initial tendency was to respond with
the total number in the array.
like "4 key" (the
use of plurals was not required; To
see a video of Alex performing click here, this video is 58 seconds in
duration, so download times will be longer then most of the videos in this
book). His previous experience with shapes was
extended to items such as "6-corner paper". He also learned to tell the
number of objects in a subset within a heterogeneous array, e.g. when asked
"How many cork?" he could answer "2" when shown a random mixture of 2 corks
and 3 keys. His ability to label cardinal sets accurately transferred to
other objects for which he knew the names but which had not been used in
numerical training. So Alex used "spoken" numbers as abstract labels. Interestingly,
when he was questioned about the number of unfamiliar objects in mixed
arrays of known and novel items, his initial tendency was to respond with
the total number in the array.
Later (Pepperberg, 1994),
the range of Alex’s vocal numerical labels was extended to include "one".
Also, his ability to give the number for a subset with a particular conjunction
of properties was tested. In each test set there were four different numbers
for the subset combinations. Test items could be in one of two colors (e.g.
green or blue) or in one of two forms (e.g. truck or key). Alex was then
asked a question about the quantity of a specific subset such as "How many
green truck?". He was able to answer with a high level of accuracy. The
aim of this study was to investigate whether Alex might have relied on
subitizing or counting to judge quantity. Subitizing was considered to
be a perceptual and preattentive mechanism by which numbers of items up
to 4 are recognized holistically. Counting, on the other hand, would require
abstraction. It was assumed to be necessary for quantities beyond the subitizing
range and to require more spatial attention. Alex was equally accurate
at judging subsets in the range of 1 to 6 items. He also had to process
items defined by the conjunction of their properties (e.g. green and
truck) when these items were scattered randomly amongst other similarly
complex objects (e.g. blue trucks, green keys, blue keys) that would have
acted as perceptual distractors. Although Pepperberg could not totally
dismiss subitizing as a potential process contributing to Alex’s performance,
she thought it was unlikely that he could easily segregate the target subset
from all the other items and clump the relevant items together. The even
distribution of errors that Alex made with both smaller and larger numbers,
together with his ability to deal with conjunctive subsets, was probably
more compatible with counting. On the other hand there was no evidence
that Alex applied numerical labels in an ordinal fashion, for instance.
Although all the principles of counting (Gelman & Gallistel, 1978)
were not directly tested in this experiment, this parrot has obviously
demonstrated an ability to respond in a flexible way to the absolute or
cardinal number of things that make up a group, or part of a group. The
extent to which parrots rely on a process like subitizing versus one like
counting is still being investigated (I. Pepperberg, pers. comm.).
"Counting", in the sense
of assessing cardinal numbers, can be expressed in quite different ways
but roughly one can distinguish two categories of behavior: counting external
items, as Alex probably did, and counting one’s own responses. Only a few
studies have investigated the latter type of behavior. Zeier (1966), for
example, explored the upper limit of pecking responses that pigeons could
deliver in a precise manner. Pigeons had to peck the first of two response
keys a specific number of times. By pecking the second key the pigeon signaled
that it had completed the pecking sequence on the first key. Zeier successively
increased the number of required pecks and found that the upper limit that
individual pigeons could produce amounted to 8, but for the majority of
the birds the upper limit was clearly below 8.
However, Zeier’s pigeons
never had to cope with different response numbers at the same time or learn,
in the way that Alex did, to link things to be counted with symbols representing
their number. To find out whether pigeons would be able to produce specific
numbers of pecks in response to given symbols, Xia, Siemann and Delius
(2000) used 6 symbols (A, N, T, 4, U, and 5, some of them rotated) that
were presented on one of the pecking keys (the "symbol" key) in a conditioning
chamber. Each symbol was associated with a certain required number of pecks.
A second key
 (the "enter" key) had to be pecked to indicate that the response
requirement on the first key had been fulfilled. If this second key was
pecked before the response requirement
on the first key was completed, or if too many pecks had been delivered
on the first key, a timeout followed (during which the houselight was turned
off). Pigeons only received food reward for the exact production of the
required number of pecks on the first key and a final single peck on the
second key. (Click here for an explanation
of the procedure, and click here for animated
illustration of the procedure). (the "enter" key) had to be pecked to indicate that the response
requirement on the first key had been fulfilled. If this second key was
pecked before the response requirement
on the first key was completed, or if too many pecks had been delivered
on the first key, a timeout followed (during which the houselight was turned
off). Pigeons only received food reward for the exact production of the
required number of pecks on the first key and a final single peck on the
second key. (Click here for an explanation
of the procedure, and click here for animated
illustration of the procedure).
After prolonged training,
6 out of 9 pigeons reached a choice performance well above chance level
for the first 4 symbols presented in a random order. Six of these birds
managed to deal with 5, and 4 animals also dealt reliably with all 6 symbols.
The mean choice performance was 79%, 84%, 74%, 68%, 53%, and 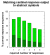 50% correct response sequences for numbers 1 to 6 respectively. These
results are shown in Figure
8. Note, that the chance level decreases with the response number
as the number of wrong alternatives increases. For example with a response
requirement of 3 there is one correct response sequence, but 4 wrong sequences,
thus chance level is 20%; with a response requirement of 6, there is one
correct, but 7 incorrect sequences, therefore chance level amounts to 12.5%.
Response distributions to each given symbol revealed that errors were more
frequent with an adjacent numerosity than with more distant numerosities
(e.g. 4 responses were more frequent than 2 when the correct number was
5).
50% correct response sequences for numbers 1 to 6 respectively. These
results are shown in Figure
8. Note, that the chance level decreases with the response number
as the number of wrong alternatives increases. For example with a response
requirement of 3 there is one correct response sequence, but 4 wrong sequences,
thus chance level is 20%; with a response requirement of 6, there is one
correct, but 7 incorrect sequences, therefore chance level amounts to 12.5%.
Response distributions to each given symbol revealed that errors were more
frequent with an adjacent numerosity than with more distant numerosities
(e.g. 4 responses were more frequent than 2 when the correct number was
5).
The task took several thousand
trials for the pigeons to acquire but nevertheless shows that these birds
are capable of associating cardinal numbers of responses with different
visual symbols for each of these numbers. The birds’ behavior was also
quite flexible since they accurately produced the required number of responses
to whichever symbol was randomly presented to them.
V.
Judging Proportion with Continuous or Discrete Quantities
Judging the number of things
is one way of estimating quantity. However, differences in quantity also
depend on other dimensions. For instance, food quantities differ not just
as a result of the number of edible items available but also because of
their sizes, volumes, weights, etc. Most of the experiments described so
far have controlled for other dimensions in order to see if birds can choose
on the basis of number alone. They obviously can do so but seem to be more
adept at judging relative differences in number than absolute amounts.
Another way of looking at relative quantities is to consider the proportions
of items in heterogeneous sets. In the experiments described so far, proportion
has been equated with the relative numerosity of two types of items in
mixed stimulus arrays (Honig & Stewart, 1989). In another study (Emmerton,
2001) pigeons were trained to discriminate differences in color proportions
within horizontal bars composed of continuous blocks of color. They were
then tested under a variety of conditions to see if they still responded
accurately to differences in the relative quantity of color when the stimulus
displays were altered.
Initially, the pigeons learned
to discriminate between a red and a green horizontal bar when these two
stimuli were presented simultaneously on a computer monitor. The ‘correct’
color was counterbalanced across birds. Responses were sensed by a touchscreen,
and a peck to the correct color led to food reward. Then the proportion
of the two colors was varied in both stimuli. If a bird chose the bar with
the greater proportion of the ‘correct’ color (e.g. red in the following
stimulus examples), it was rewarded. If it chose the bar with the complementary
lesser proportion of ‘correct’ color a timeout period followed. If the
pr oportion
of red to green was equal in both bars, one of the stimuli was arbitrarily
programmed to be the correct one but the bird had to guess which one it
was. For examples of the oportion
of red to green was equal in both bars, one of the stimuli was arbitrarily
programmed to be the correct one but the bird had to guess which one it
was. For examples of the 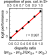 stimuli the birds saw across a series of trials, click
here. The accuracy with which the birds discriminated the paired bars
was correlated with the color proportions in the bars (see Figure
9). When there was no difference in proportion, their performance
was at chance level. Since a non-linear discrimination function was obtained
when behavioral scores were measured on a scale of percentage of correct
choices, these behavioral measures were linearized by converting the scores
to a logit scale (defined as ln(% correct/(100 - % correct)); Macmillan
& Creelman, 1991).
stimuli the birds saw across a series of trials, click
here. The accuracy with which the birds discriminated the paired bars
was correlated with the color proportions in the bars (see Figure
9). When there was no difference in proportion, their performance
was at chance level. Since a non-linear discrimination function was obtained
when behavioral scores were measured on a scale of percentage of correct
choices, these behavioral measures were linearized by converting the scores
to a logit scale (defined as ln(% correct/(100 - % correct)); Macmillan
& Creelman, 1991).
The stimuli presented in
this initial condition were deliberately different from those used by Honig
and Stewart (1989, 1993). Whereas they had used arrays of discrete items,
this new experiment used stimuli consisting of continuous areas of color.
In this case, proportion was no longer equated with the relative numerosity
of component items but the results of both experiments were very similar:
as the difference in the proportion of colored areas or discrete items
decreased so did the accuracy of the birds’ discrimination. One of the
questions in this recent study was whether the pigeons would still respond
to changes in proportion when the stimuli were changed to consist of arrays
that were similar to those used by Honig and Stewart. So in one part of
the study, the birds were presented not with paired horizontal bars but
with arrays of small red and green rectangles. There were two types of
arrays. In one type the rectangles were configured in regular matrices.
In another type the arrangement of the rectangles within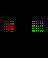 the arrays was irregular to break up any potential texture effects. To
see examples of the stimuli as they appeared across trials, click
here. The birds transferred to these altered stimuli without any difficulty
and their accuracy in choosing the array with the greater
the arrays was irregular to break up any potential texture effects. To
see examples of the stimuli as they appeared across trials, click
here. The birds transferred to these altered stimuli without any difficulty
and their accuracy in choosing the array with the greater  proportion of ‘correct’ color in it still depended on the difference in
color proportion between the paired arrays (see Figure
10). In this case, as in Honig and Stewart’s experiments, color
proportion is synonymous with the relative numerosity of red and green
rectangles. So proportion, irrespective of whether it refers to the relative
number of discrete items in a mixture, or to a continuous dimension such
as the relative length or area of different constituents, is another abstract
property on which judgments about quantity are based.
proportion of ‘correct’ color in it still depended on the difference in
color proportion between the paired arrays (see Figure
10). In this case, as in Honig and Stewart’s experiments, color
proportion is synonymous with the relative numerosity of red and green
rectangles. So proportion, irrespective of whether it refers to the relative
number of discrete items in a mixture, or to a continuous dimension such
as the relative length or area of different constituents, is another abstract
property on which judgments about quantity are based.
Other experiments on numerical
discrimination suggest that animals discriminate relative rather than absolute differences
in numerosity. For instance, Boysen, Berntson, Hannan and Cacioppo (1996)
found high correlations between chimpanzees’ discrimination accuracy and
the disparity ratio of numerosity with real objects (candies or pebbles).
In that context, the disparity ratio was defined as the difference in number
between paired stimuli divided by the sum of their numbers. In the experiment
on proportion discrimination with pigeons, the stimulus conditions described
so far utilized stimuli in which the proportions of ‘correct’ color in
the paired positive and negative stimuli were complementary. Disparity
ratio in this experiment could be defined as the difference in the proportions
of ‘correct’ color in paired stimuli divided by the sum of those proportions.
However, with complementary values, this would be the same as calculating
the absolute difference in color proportion within a stimulus pair. So
another stimulus condition was devised to test whether the birds’ discrimination
performance was really related to the relative difference in proportion,
or disparity ratio.
 The
stimuli again consisted of horizontal bars but there were three sets of
stimuli intermixed within sessions. Click
here for examples of the stimuli. One set (the S+/S- set) was the same
as in the initial condition for examining proportion discrimination – color
proportions varied in a complementary fashion in positive and negative
stimuli. Choice of the S+ bar with the greater proportion of ‘correct’
color in it was rewarded. In another (S+/0.5) set, the proportion of ‘correct’
color in one bar varied as it did in the S+ bars on rewarded trials. The
other bar always contained equal proportions of red and green. For this
set, a bird’s response was registered as correct if it chose the "S+" bar
with the greater, variable proportion of ‘correct’ color (or guessed the
arbitrarily ‘correct’ stimulus in the case of both bars containing equal
proportions of color). In the third (0.5/S- ) set, one bar again contained
equal amounts of red and green. The proportion of the two colors varied
in the other one so that on average this other bar contained a lesser proportion
of the ‘correct’ color as in the S- bars of rewarded trials. So for this
third stimulus set the correct response was to avoid the bar that had the
lesser proportion of ‘correct’ color and choose the one with the greater
proportion (the 0.5 bar). Whenever a pair of stimuli from the second or
third set appeared, the birds’ choices were recorded as correct or incorrect
ones but t The
stimuli again consisted of horizontal bars but there were three sets of
stimuli intermixed within sessions. Click
here for examples of the stimuli. One set (the S+/S- set) was the same
as in the initial condition for examining proportion discrimination – color
proportions varied in a complementary fashion in positive and negative
stimuli. Choice of the S+ bar with the greater proportion of ‘correct’
color in it was rewarded. In another (S+/0.5) set, the proportion of ‘correct’
color in one bar varied as it did in the S+ bars on rewarded trials. The
other bar always contained equal proportions of red and green. For this
set, a bird’s response was registered as correct if it chose the "S+" bar
with the greater, variable proportion of ‘correct’ color (or guessed the
arbitrarily ‘correct’ stimulus in the case of both bars containing equal
proportions of color). In the third (0.5/S- ) set, one bar again contained
equal amounts of red and green. The proportion of the two colors varied
in the other one so that on average this other bar contained a lesser proportion
of the ‘correct’ color as in the S- bars of rewarded trials. So for this
third stimulus set the correct response was to avoid the bar that had the
lesser proportion of ‘correct’ color and choose the one with the greater
proportion (the 0.5 bar). Whenever a pair of stimuli from the second or
third set appeared, the birds’ choices were recorded as correct or incorrect
ones but t hey
were given neither reward nor timeout, so these were all test trials. For
these two test sets, the disparity ratio of color proportion was no longer
the same as the absolute difference in proportion values. The accuracy
of the birds’ choices for all three sets of stimuli was closely correlated
with changes in the disparity ratio of color proportion (see Figure
11). hey
were given neither reward nor timeout, so these were all test trials. For
these two test sets, the disparity ratio of color proportion was no longer
the same as the absolute difference in proportion values. The accuracy
of the birds’ choices for all three sets of stimuli was closely correlated
with changes in the disparity ratio of color proportion (see Figure
11).
VI.
Models and Mechanisms for Numerical Processing
Various models and mechanisms have been proposed to account for animals'
(and presumably humans') ability to assess numerical quantities. Pacemaker-accumulator
models, and a stimulus control model were designed to explain how different
numbers of sequential events are processed. Subitizing, and a neuronal
filtering model on the other hand were primarily intended to account for
the numerical processing of visual arrays.
Pacemaker-Accumulator
Models
This model has been developed
by Roberts and Mitchell (1994) as an extension of the pacemaker-accumulator
model previously proposed by Meck and Church (1983). According to this
model, the same, or similar, mechanisms are used for timing and counting,
since, in both pigeons and rats, behavioral results for time and number
are similar when the animals could have learned about either dimension.
The basic mechanism in this model is a pacemaker, or oscillator, that emits
pulses at a fixed rate. These pulses are then switched into other mechanisms.
In Roberts’ version of the model, the pulses can be routed simultaneously
into two different accumulators. One type of switch closes at the start
of a sequence of events and continues to allow pulses to be accumulated
until the sequence finishes. This channel is used for timing. The other
type of switch closes for a brief, fixed period when each event in the
series occurs. So the number of pulses that  collect in a separate accumulator
– the current value of its ‘contents’ – is proportional to the number of
sequential events that have occurred. This channel is used for "counting".
Information about the
total numbers of pulses in each type of accumulator is then transmitted
to different compartments of working memory. By comparing the current information
in working memory with previously stored information in reference memory,
an animal decides how to behave, e.g. whether to peck a left or a right
key. The main features of the ‘counting’ channel in this type of model
are illustrated schematically in Figure
12.
collect in a separate accumulator
– the current value of its ‘contents’ – is proportional to the number of
sequential events that have occurred. This channel is used for "counting".
Information about the
total numbers of pulses in each type of accumulator is then transmitted
to different compartments of working memory. By comparing the current information
in working memory with previously stored information in reference memory,
an animal decides how to behave, e.g. whether to peck a left or a right
key. The main features of the ‘counting’ channel in this type of model
are illustrated schematically in Figure
12.
The model was designed to
account for counting and timing with sequential events – series of light
flashes, sequences of tones, or a run of behavioral responses emitted by
the animal itself. At first, it seems to have little to do with a pigeon’s
ability to discriminate the number of items in visual arrays since these
items are presented simultaneously. However, if birds in fact scan arrays,
as the effects of changes in dot density suggest (Emmerton, 1998), then
the pacemaker-accumulator model could also apply to numerosity discrimination
with those types of stimuli.
Mathematical
Model of Stimulus Control Effects
An entirely different model
has been proposed by Keen and Machado (1999). This model shows how birds
make different choices depending on the relative numbers of events of two
types, e.g. red vs. green lights presented sequentially. In contrast to
all the other models of number-related behavior, however, this model does
not assume that birds in any sense ‘count’, store numerical representations,
remember the actual number of stimuli they have seen, or have an
internal processing mechanism for numerosity itself.
Essentially, the model assumes
that when a series of similar events occurs (like 5 successive red-light
stimuli), the probability of the bird’s performing one behavior (e.g. pecking
one key) increases linearly by a constant amount for each of the stimuli
shown. When a series of different events occurs, these other events
increase the likelihood of the animal’s making an alternative response
(e.g. peck the other key). The amount of stimulus control (influence on
responding by these stimuli) depends on the number of events of each type,
but not because the animal counts or performs any numerical calculations.
When each series of stimuli is no longer present, the memory of the cumulative
stimulus effects for that series decays exponentially. There are two parameters
in the model. One is the relative incremental effect on stimulus control
of each stimulus in the first versus the second series. The effects of
the first stimuli are assumed to interfere in part with the effects of
the second set (proactive interference). The other parameter is decay following
stimulus events. Decay refers to the degrading effects of the passage of
time on a memory trace for a particular type of stimulus, the retroactive
interference effects of presenting one type of stimulus after another type,
or both. The bird’s choice of response depends on the net effectiveness
of one series compared with the other when the bird has to decide what
to do.
The model can account for
the effect of relative numbers of sequential stimuli or events on birds’
choices. For instance, it provided a good fit to behavioral data that conformed
to Weber’s law. The mathematical model also successfully predicted recency
and primacy effects – whether later or earlier stimulus events have more
influence on behavioral choices. It remains to be seen, though, how it
would explain birds’ discrimination of numerosity with simultaneously presented
arrays of items (even if the items themselves are scanned). When birds
have to choose between arrays, it is not clear what role the two parameters
of the mathematical model would play. Similarly, it is unclear how the
model would explain birds’ conditional discrimination when only a single
array is presented but the animals’ choices are related to the array’s
numerosity value. With the latter type of stimulus displays, discrimination
performance is remarkably robust, even with arrays of inhomogeneous items,
or when the types of items are altered, or novel stimuli are introduced.
Furthermore, the model is designed to deal with discriminations of the
‘more’ vs. ‘less’ type and so would not be applicable to judgments about
the absolute number of things or events (see section IV).
Subitizing
Other types of mechanisms
have been proposed to explain how animals make judgments about the numerosity
of items in arrays. One of the earliest proposals was that animals assess
small numbers by a process of subitizing. Subitizing refers to a type of
pattern recognition by which quantities of about 1 to 4 items are rapidly
assessed. For example, 2 dots form the end points of a straight line. Three
dots either fall in a straight line or else define the corners of a triangle.
Subitizing was originally thought to be a mechanism, separate from enumeration,
by which humans make quick and accurate estimates of small numbers of things
(Kaufman, Lord, Reese & Volkmann, 1949). People were reported to show
very short reaction times while accurately judging up to 4 things whereas
reaction times increased progressively when they had to assess greater
numbers of items. However, these differences in reaction times have been
called into question (Balakrishnan & Ashby, 1992). In animals, the
necessary information about reaction times is lacking (Miller, 1993). Also,
pigeons can make relative numerosity judgments even when the arrays consist
of entirely novel numbers of dots, as Emmerton et al. (1997) showed in
the study of serial ordering effects. In that case, the birds had no opportunity
to learn about the patterns that 3, 4 or 5 dots can form. So subitizing,
if it exists as a separate process, is neither necessary nor sufficient
to account for birds’ numerosity judgments. On the other hand, the extent
to which pattern recognition enables birds to make choices about familiar
array configurations is unclear at the moment.
Neuronal
Filtering Model
Dehaene and Changeux (1993)
proposed a different model based on neuronal filtering mechanisms. In their
model, an array of objects or elements is first coded as different clusters
of activity in a network, such as the retina. Subsequently each cluster
of activity from the input level is filtered so that only item location
within the array is encoded, but other features, such as the size of each
object, become irrelevant. The activity from each unit at this stage is
then summated  and transferred to the next neuronal level. There, the summed activity
is gated by other units which set different threshold levels. Activation
that exceeds a particular threshold is then transmitted to a final neuronal
level. At this level, units respond to only a selected range of activity
values so that these units function as the numerosity detectors (see Figure
13).
and transferred to the next neuronal level. There, the summed activity
is gated by other units which set different threshold levels. Activation
that exceeds a particular threshold is then transmitted to a final neuronal
level. At this level, units respond to only a selected range of activity
values so that these units function as the numerosity detectors (see Figure
13).
This model was primarily
designed to explain how judgments are made about the numbers of items seen
simultaneously in arrays. So it is easiest to see how it would explain
the parallel processing of numbers of objects, rather than the serial processing
of events. However, Dehaene and Changeux suggest that, with the addition
of some form of sensory store, it could also be modified to deal with sequentially
presented stimuli such as light flashes. With this type of modification
it would still apply if pigeons serially scan the items in arrays, as suggested
earlier.
Variance
Assumptions
At present, it is not clear
whether a pacemaker-accumulator model or a neuronal filtering model best
accounts for animals’ numerical abilities (if indeed either one applies).
Both models assume some inherent variability at the different 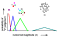 processing levels. This means that, although an animal’s average estimate
about number might tally well with the actual number of items it encounters,
its repeated estimates will show some variance about a mean value. For
both models it is assumed that this variance will become greater as the
number of items or events to be assessed increases. This idea is illustrated
in Figure 14.
This link between variance and number can explain why pigeons found it
easier to discriminate arrays of 1, 2, 3 and 4 items in the experiment
on serial ordering (Emmerton et al., 1997), but arrays of 5, 6 or 7 dots
were less easily differentiated. The assumption of variability made by
both processing models also corresponds to evidence that Weber’s law applies
to numerosity judgments. Note, however, that Keen and Machado (1999) report
data that by and large conform to Weber’s law, although their mathematical
model includes no variance assumptions.
processing levels. This means that, although an animal’s average estimate
about number might tally well with the actual number of items it encounters,
its repeated estimates will show some variance about a mean value. For
both models it is assumed that this variance will become greater as the
number of items or events to be assessed increases. This idea is illustrated
in Figure 14.
This link between variance and number can explain why pigeons found it
easier to discriminate arrays of 1, 2, 3 and 4 items in the experiment
on serial ordering (Emmerton et al., 1997), but arrays of 5, 6 or 7 dots
were less easily differentiated. The assumption of variability made by
both processing models also corresponds to evidence that Weber’s law applies
to numerosity judgments. Note, however, that Keen and Machado (1999) report
data that by and large conform to Weber’s law, although their mathematical
model includes no variance assumptions.
Weber’s
Law and Judgments of Numerical Difference
Weber's law basically says
that the ability to discriminate two stimuli is a ratio function
of the stimuli, rather than a function of the absolute difference between
them. Weber’s law has often been applied in measuring sensory abilities.
For instance, if we (or any other vertebrate species) have to judge whether
one light is brighter than another, or one sound is louder than another,
our ability to choose the brighter or the louder stimulus depends on the
value of the reference stimulus. The brighter the reference light (or the
louder the reference sound) the greater must be the difference between
it and a comparison stimulus for us to accurately tell the two apart. In
addition, Weber’s law operates in a variety of situations that require
discriminations of abstract cognitive dimensions. This law underlies discrimination
of time as well as number when birds have to judge how many pecks they
have made or how long a response series lasts (Fetterman, 1993). It also
applies to temporal and numerical judgments made by rats when they are
presented with tone series (Gibbon, 1977; Meck & Church, 1983). The
results of the experiments reported here on the discrimination of color
proportion (see Figure 11 in section V) conform to Weber's law. Transformation
of the data from a recent experiment on numerosity discrimination indicates
that Weber's law applies to birds' discrimination of visual arrays too.
In that experiment some pigeons
were trained to choose consistently an array containing ‘more’ dots while
others always had to choose the array with ‘less’ dots in it. (These opposite
training conditions were designed to see if birds are biased to choose
greater numbers, as will be discussed in section VII.) If numerosity discrimination
obeys Weber’s law we would expect that as the number of items in the ‘correct’
array increases, so the difference in number that can be discriminated
from this reference amount will increase proportionally. To see whether
Weber’s law applies to the results in this experiment, numerical disparity
ratios were calculated for all the array pairs that were used. As in the
experiments by Boysen et al. (1996), a disparity ratio is defined as the
difference in numbers of dots between paired arrays divided by the sum
of all the dots in a stimulus pair. The scores of discrimination accuracy
were again transformed to a logit scale. Linear regression analyses were
then applied to these transformed data. From the start, the results from
the birds trained to choose ‘more’ followed this linear relationship. At
the start of training, the birds that had to choose ‘less’ did not show
this pattern of results.  These initial data are shown in Figure
15. However, the results of pigeons in the ‘less’ group were due
to the birds' bias to choose the more numerous array. A linear relationship
between logit performance scores and numerosity disparity ratios did emerge
after extended training with familiar stimuli had enabled the birds to
overcome their bias. So long as their predisposition to choose the greater
number did not interfere with the birds’ choice accuracy, the pigeons discriminated
the arrays as Weber’s law would predict and differentiated the arrays on
the basis of the relative difference in the numbers of dots they
contained.
These initial data are shown in Figure
15. However, the results of pigeons in the ‘less’ group were due
to the birds' bias to choose the more numerous array. A linear relationship
between logit performance scores and numerosity disparity ratios did emerge
after extended training with familiar stimuli had enabled the birds to
overcome their bias. So long as their predisposition to choose the greater
number did not interfere with the birds’ choice accuracy, the pigeons discriminated
the arrays as Weber’s law would predict and differentiated the arrays on
the basis of the relative difference in the numbers of dots they
contained.
Various results now support
the idea that Weber’s law, which is incorporated in the current models
of "counting", applies to numerical discriminations. Whether or not any
of these models prove to be valid, this seems to be a feature that any
future models must also include.
VII.
Do Birds’ Numerical Abilities Have Any Functional Significance?
Dating back to the earliest
anecdotes about animals’ potential counting ability, there has been the
implicit assumption that being able to keep track of the number of things
must have survival value for any animal that can do so. A behavioral trait
need not necessarily have functional significance (see Gould & Lewontin,
1979). For instance, being able to estimate numerosity may be just a spin-off
of very precise timing abilities. However, there are some situations in
which it might be advantageous to be able to differentiate numerosity.
One situation that comes to mind is foraging. When an animal has to make
feeding choices it may be useful for it to estimate the number of food
items available in different patches. Another situation is in keeping track
of what other animals in a group are doing. Some observations indicate
that birds use numerosity discrimination to assess how many other members
of a flock are currently engaged in watching out for predators, rather
than in attending to the business of gathering food.
In its natural environment,
an animal is constantly faced with the problem of optimizing its energy
intake, and being able to choose the larger of alternative food patches
may contribute to survival. However, being able to assess the number of
items in a food-patch is no guarantee of that patch being the best one
to choose. Optimal foraging theory (Krebs, 1978) instead suggests that
several factors determine how an animal maximizes its energy budget in
the wild. The ability to discriminate and choose the larger number of food
items in seed-patches or clumps of berries most likely serves as a "rule
of thumb" (Krebs & McCleery, 1984; Shettleworth, 1984). This means
that choosing the greater number of food items often, but not always, leads
to a better payoff.
These ideas suggested that
a bird, if given a choice between two arrays, should more readily choose
the one containing the greater number of items. Such a bias had already
been mentioned by Koehler (1941). When he trained a pigeon to choose one
of two seed patches, placed at opposite ends of a strip of cardboard, he
noticed a spontaneous tendency by the bird to approach the larger amount,
even if the ‘correct’ one for the bird to eat was the less numerous patch.
So in an experiment (mentioned in the previous section on Weber's law)
pigeons were trained to discriminate between paired arrays of seed-like
dots. Choice of the correct array led to a constant amount of food reward.
The numbers of dots in the array pairs  varied across trials. But some birds always had to choose the more numerous
array to obtain reward whereas the other birds had to choose the less numerous
array. Otherwise training conditions were identical. As expected, the group
that was trained to choose ‘more’ performed better in this task during
the early stages of training than the group that was trained to choose
‘less’ (see Figure
16). With extended training, both groups reached similar levels
of discrimination accuracy. Then a transfer phase started.
varied across trials. But some birds always had to choose the more numerous
array to obtain reward whereas the other birds had to choose the less numerous
array. Otherwise training conditions were identical. As expected, the group
that was trained to choose ‘more’ performed better in this task during
the early stages of training than the group that was trained to choose
‘less’ (see Figure
16). With extended training, both groups reached similar levels
of discrimination accuracy. Then a transfer phase started.
In the transfer sessions,
some non-rewarded trials included new stimulus arrays. Not only were the
patterns of dots in the test arrays novel to the birds, but also pairs
of arrays were matched in brightness. Although both groups of birds were
still equally accurate at choosing correctly on familiar training trials,
differences between the groups re-emerged  on the test trials. The birds that were trained to choose ‘more’ were quite
accurate in choosing the more numerous test arrays. However, the group
that was trained to choose ‘less’ was poorer at choosing the less numerous
novel arrays. The results are shown in Figure
17. When trained to choose an artificial ‘patch’ that was
associated with food reward, the birds seemed to be biased from the start
of the experiment to choose the array with the greater number of dots in
it. Even though the birds trained to choose ‘less’ could learn to overcome
this bias with familiar stimuli, the predisposition to choose the more
numerous array became apparent once more in the test trials.
on the test trials. The birds that were trained to choose ‘more’ were quite
accurate in choosing the more numerous test arrays. However, the group
that was trained to choose ‘less’ was poorer at choosing the less numerous
novel arrays. The results are shown in Figure
17. When trained to choose an artificial ‘patch’ that was
associated with food reward, the birds seemed to be biased from the start
of the experiment to choose the array with the greater number of dots in
it. Even though the birds trained to choose ‘less’ could learn to overcome
this bias with familiar stimuli, the predisposition to choose the more
numerous array became apparent once more in the test trials.
These results suggest that
birds might indeed use their numerical abilities in foraging. However,
in this particular experiment the birds did not eat the arrays, and the
reward they obtained was a constant amount of food. Other experiments with
both rats and birds support the idea that numerosity discrimination might
operate as a ‘rule of thumb’ in deciding between foraging opportunities,
even when the weight of reward is equated. For instance, chickens that
were trained to seek food at the end of a runway ran faster when the reward
was presented as 4 pieces of a single kernel of corn rather than as 1 whole
grain. They also were more accurate at choosing the correct arm of a T-maze
when the reward was presented in multiple pieces rather than a single one
(Wolfe & Kaplon, 1941). Contrary to these results, Olthof and Roberts (2000)
found that pigeons rely on the overall mass, rather than the number of items, to
assess the relative quantity of food rewards. However, the birds did not
visually discriminate between food rewards directly. Rather, they had to choose
between symbols (colored shapes) that represented specific amounts of reward.
Numerical discrimination
may also be of functional significance to birds that forage in flocks and
switch between searching for food and scanning the environment for predators.
Observations of a variety of species have shown that birds generally spend
a greater amount of time eating rather than being vigilant for predators
as flock size increases (Elgar, 1989). However, several other factors also
influence vigilance behavior. These include flock geometry – whether birds
are aligned with each other or feeding in a circle (Bekoff, 1995). Another
factor is whether other members of the flock are visible or are obscured
by obstacles such as rocks or trees (see Elgar, 1989). A model of vigilance
behavior (Bahr & Bekoff, 1999) incorporates the ability of birds to
categorize their conspecifics’ behavior as either feeding or scanning and
to discriminate the numbers of individuals showing each type of behavior.
The model assumes that a bird monitors up to 8 of its nearest neighbors
in a flock. Dependent on the relative number of birds that it can see feeding
or scanning it will decide whether to forage or to be vigilant. The small
number range seems to be important since observations show that, once flock
size exceeds about 10 birds, further increases in the number of birds do
not affect the proportion of time that an individual spends scanning (Elgar,
Burren & Posen, 1984). The ability to assess the number of conspecifics
is not the only factor that influences vigilant behavior, but, as with
other aspects of foraging, it appears to be an important contributory factor.
VIII.
Conclusions
This chapter has concentrated
on the ability of birds to deal with different aspects of number and quantity
when some form of visual stimulus is involved. This focus tends to conceal
at least two points. One is that birds also differentiate number in contexts
in which visual stimuli are unimportant, for instance, when they discriminate
the relative numbers of responses they emit on different fixed-ratio schedules
(Fetterman, 1993). The other point concerns the striking similarities between
avian abilities and those of other species that have been tested on numerical
tasks. For example, chimpanzees that have to choose between two arrays
of real objects (candies or pebbles) are biased, as pigeons are, to choose
the array containing ‘more’ items (Boysen & Berntson, 1995; Boysen,
Berntson, Hannan & Cacioppo, 1996). In chimpanzees this bias is overcome,
by the way, when they have to choose between Arabic numerals that stand
for different numbers of candies as reward, a possibility that has not
yet been tested with birds. Both parrots and pigeons can learn to associate
arbitrary symbols with precise numbers of objects or events (but see Olthof
& Roberts, 2000). These types
of associations have been demonstrated in primates (monkeys: Olthof, Iden
& Roberts, 1997, chimpanzees: Boysen, 1993, and of course humans: Gelman
& Gallistel, 1978). Pigeons seem to order arrays containing different
numbers of dots in a serial fashion (Emmerton et al., 1997). Serial ordering
of visual arrays that vary in their numerosities has been demonstrated
more explicitly in rhesus monkeys (Brannon & Terrace, 1998, 2000).
Even the earliest anecdotal
speculations about animals’ "counting" behavior implied that the ability
to make numerical discriminations is functionally significant. Choice biases
seen in the artificial foraging situation of experiments that use food-rewards
are one reflection of this. As long as there are no other factors (such
as predators or aggressive competitors) to complicate the picture, it is
often advantageous to choose the items that are greater in number. It may
even be adaptive for an animal to be able to judge relative differences
in number or quantity more easily than absolute amounts. This conjecture
is based on the amounts of training required for birds to master different
tasks, and considerations of how numerical abilities might be used in an
animal's natural habitat. Most studies so far have tested birds’ performance
in assessing numerosity differences rather than absolute or cardinal numbers.
Birds learn quite readily, especially with visual stimuli, to differentiate
‘more’ from ‘less’, ‘many’ from ‘few’, or a mixture containing a greater
proportion of one feature from a mixture containing a smaller proportion.
In the few studies dealing with cardinal numbers of objects or responses
the birds have required extensive training. However, it is not yet clear
whether this is because the animals have to assess the exact numbers of
items they see or pecks they should emit, or whether the additional requirement
of associating a precise amount with a numerical symbol is what really
taxes them. The ability to make relative judgments of number, as of other
dimensions, may be of more general utility though. Being able to assess
where there is more food, where there are fewer competitors, which tree
contains more ripe fruit, etc. may often be more important than knowing
the exact number of each of these things. But as the crow anecdote suggested,
there may nevertheless be situations in which being able to keep track
of exact small numbers is also essential for survival!
Unresolved
Issues
In spite of the progress
achieved in our understanding of different facets of birds’ numerical abilities,
several issues still have to be resolved. One is the extent to which they
integrate number with other aspects of quantity when they discriminate
visual features of their environment. Another issue is whether birds deal
with small compared with larger numbers of items or events in a similar
fashion or whether there are any differences in their behavior across the
number range. Can they, for instance, really count small numbers of things
(according to the principles outlined by Gelman and Gallistel, 1978) but
make only relative judgments of larger amounts? Perhaps related to this
is still the question of whether there is just one common mechanism underlying
numerical behavior (and, if so, which one), or are there several mechanisms
that are employed to a greater or lesser extent in different situations?
And how do birds, and other animals, utilize their ability to discriminate
number and quantity in their natural environment? Perhaps some of the ongoing
research in this area of animal cognition will soon enable us to understand
this remarkable avian capability even better.

IX.
References
Alsop, B. & Honig, W. K. (1991). Sequential stimuli and relative numerosity
discriminations in pigeons. Journal of Experimental Psychology: Animal
Behavior Processes, 17, 386-395.
Bahr, D. B. & Bekoff, M. (1999). Predicting flock vigilance from simple
passerine interactions: modeling with cellular automata. Animal Behaviour,
58, 831-839.
Balakrishnan, J. D. & Ashby, F. G. (1992). Subitizing:
Magical numbers or mere superstition? Psychological Research, 54,
80-90.
Bekoff, M. (1995). Vigilance, flock size, and flock geometry: information
gathering by western evening grosbeaks (Aves, Fringillidae). Ethology,
99, 150-161.
Boysen, S. T. (1993). Counting in chimpanzees: Nonhuman principles and
emergent properties of number. In S. T. Boysen & E. J. Capaldi (Eds.)
The
development of numerical competence: Animal and human models. (pp. 39-59). Hillsdale,
NJ: Erlbaum.
Boysen, S. T. & Berntson, G. G. (1989).
Numerical competence in a chimpanzee (Pan troglodytes). Journal
of Comparative Psychology, 103, 23-31.
Boysen, S.T. & Berntson, G.G. (1995). Responses
to quantity: perceptual versus cognitive mechanisms in chimpanzees (Pan
troglodytes). Journal of Experimental Psychology: Animal Behavior
Processes, 21, 82-6.
Boysen, S. T., Berntson, G. G., Hannan, M. B., &
Cacioppo, J. T. (1996).
Quantity-based
interference and symbolic representations in chimpanzees (Pan troglodytes).
Journal
of Experimental Psychology: Animal Behavior Processes, 22, 76-86.
Boysen, S. T. & Capaldi, E. J. (1993). The development of numerical
competence: Animal and human models. (pp. 39-59). Hillsdale, NJ: Erlbaum.
Brannon, E. M. & Terrace, H. S. (1998). Ordering
of the numerosities 1 to 9 by monkeys. Science, 282, 746-749.
Brannon, E.M. & Terrace, H.S. (2000). Representation
of the numerosities 1-9 by rhesus macaques (Macaca mulatta).
Journal
of Experimental Psychology: Animal Behavior Processes, 26, 31-49.
Candland, D. K. (1993). Feral children and clever animals: Reflections
on human nature. New York, NY: Oxford University Press.
Capaldi, E J. & Miller, D. J. (1988). Counting in rats: Its functional
significance and the independent cognitive processes that constitute it.
Journal
of Experimental Psychology: Animal Behavior Processes, 14, 3-17.
Davis, H. & Memmott, J. (1982). Counting behavior in animals: A critical
evaluation. Psychological Bulletin, 92, 547-571.
Davis, H. & Pérusse, R. (1988). Numerical competence in animals:
Definitional issues, current evidence, and a new research agenda. Behavioral
and Brain Sciences, 11, 561-615.
Dehaene, S. & Changeux, J.-P. (1993). Development of elementary numerical
abilities: A neuronal model. Journal of Cognitive Neuroscience, 5,
390-407.
Elgar, M A., Burren, P. J. & Posen, M. (1984). Vigilance and perception
of flock size in foraging house sparrows. Passer domesticus L., Behaviour,
90, 215-223.
Emmerton, J. (1998). Numerosity differences and effects of stimulus density
on pigeons’ discrimination performance. Animal Learning and Behavior,
26, 243-256.
Emmerton, J. (2001). Pigeons’ discrimination of color proportion in computer-generated
visual displays. Animal Learning and Behavior, 29, 21-35.
Emmerton, J. & Delius, J. D. (1993). Beyond sensation: Visual cognition
in pigeons. In H. P. Zeigler & H.-J. Bischof (Eds.) Vision, brain,
and behavior in birds (pp. 377-390). Cambridge, MA: MIT Press.
Emmerton, J., Lohmann, A., &
Niemann, J. (1997). Pigeons’ serial ordering
of numerosity with visual arrays. Animal Learning & Behavior, 25,
234-244.
Fetterman, J.G. (1993). Numerosity discrimination: Both time and number
matter. Journal of Experimental Psychology: Animal Behavior Processes,
19, 149-164.
Gelman, R. & Gallistel, C. R. (1978). The child’s understanding
of number. Cambridge, MA: Harvard University Press.
Gibbon, J. (1977). Scalar expectancy theory and Weber’s law in animal timing.
Psychological
Review, 84, 279-325.
Gould, S. J. & Lewontin, R. C. (1979). The spandrels of San Marco and
the Panglossian paradigm: a critique of the adaptationist programme. Proceedings
of the Royal Society of London – Series B: Biological Sciences, 205,
581-598.
Honig, W. K. & Stewart, K. E. (1989). Discrimination of relative numerosity
by pigeons. Animal Learning & Behavior, 17, 134-146.
Honig, W. K. & Stewart, K. E. (1993). Relative numerosity as a dimension
of stimulus control: The peak shift. Animal Learning & Behavior,
21, 346-354.
Kaufman, E. L., Lord, M. W., Reese, T. W. & Volkmann, J. (1949). The
discrimination of visual number. American Journal of Psychology, 62,
489-525.
Keen, R. & Machado, A. (1999). How
pigeons discriminate the relative frequency of events. Journal of
the Experimental Analysis of Behavior, 72, 151-175.
Knorn, H.-J. (1987). Visuelle
Diskriminationsleistung von Tauben und Menschen beim simultanen
Punktmengenvergleich. [Visual discrimination performance of pigeons and humans
when simultaneously comparing dot quantities.] Unpublished Diplomarbeit, Ruhr-Universität
Bochum, Bochum, Germany.
Koehler, O. (1941). Vom Erlernen unbenannter Anzahlen bei Vögeln.
[On the learning of unnamed numerosities by birds.] Die Naturwissenschaften,
29, 201-218.
Koehler, O. (1943). "Zähl"-Versuche an einem Kolkraben und Vergleichsversuche
an Menschen. ["Counting" experiments on a raven and comparative experiments
on humans.] Zeitschrift für Tierpsychologie, 5, 575-712.
Krebs, J. R. (1978). Optimal foraging: Decision rules for predators. In
J. R. Krebs & N. B. Davies (Eds.) Behavioural ecology: An evolutionary
approach (pp. 23-63). Oxford, UK: Blackwell.
Krebs, J. R. & McCleery, R. H. (1984). Optimization in behavioural
ecology. In J. R. Krebs & N. B. Davies (Eds.) Behavioural ecology:
An evolutionary approach (2nd, ed., pp.91-121). Oxford, UK: Blackwell.
Macmillan, N. A. & Creelman, C. D. (1991). Detection theory: A user’s
guide. Cambridge, MA: Cambridge University Press.
Meck, W. H. & Church, R. M. (1983). A
mode control model of counting and timing processes. Journal of
Experimental Psychology: Animal Behavior Processes, 9, 320-334.
Miller, D. J. (1993). Do animals subitize? In S. T. Boysen & E. J.
Capaldi (Eds.) The development of numerical competence: Animal and human
models. (pp. 149-169). Hillsdale, NJ: Erlbaum.
Olthof, A., Iden, C. M., & Roberts, W. A. (1997). Judgments
of ordinality and summation of number symbols by squirrel monkeys (Saimiri sciureus). Journal of Experimental Psychology: Animal Behavior
Processes, 23, 325-339.
Pepperberg, I. M. (1983). Cognition in the African Grey parrot: Preliminary
evidence for auditory/vocal comprehension of the class concept. Animal
Learning & Behavior, 11, 179-185.
Pepperberg, I. M. (1987). Evidence for conceptual quantitative abilities
in the African Grey parrot: Labeling of cardinal sets. Ethology, 75,
37-61.
Pepperberg, I. M. (1994). Numerical competence in an African Gray parrot
(Psittacus erithacus). Journal of Comparative Psychology, 108,
36-44.
Porter, J. P. (1904). A preliminary study of the psychology of the English
sparrow. The American Journal of Psychology, 15, 313-346.
Rilling, M. (1993). Invisible counting animals: A history of contributions
from comparative psychology, ethology, and learning theory. In S. T. Boysen
& E. J. Capaldi (Eds.) The development of numerical competence:
Animal and human models. (pp. 3-37). Hillsdale, NJ: Erlbaum.
Roberts, W. A. & Boisvert, M. J. (1998). Using the peak procedure to
measure timing and counting processes in pigeons. Journal of Experimental
Psychology: Animal Behavior Processes, 24, 416-430.
Roberts, W. A., Macuda, T. & Brodbeck, D. R. (1995). Memory for number
of light flashes in the pigeon. Animal Learning & Behavior, 23,
182-188.
Roberts, W. A. & Mitchell, S. (1994). Can a pigeon simultaneously process
temporal and numerical information? Journal of Experimental Psychology:
Animal Behavior Processes, 20, 66-78.
Shettleworth, S. J. (1984). Learning and behavioural ecology.
In J. R.
Krebs & N. B. Davies (Eds.) Behavioural ecology: An evolutionary approach. (2nd ed. pp. 170-194). Oxford: Blackwell.
Thorpe, W. H. (1963). Learning and instinct in animals (2nd
ed.). London: Methuen.
Wesley, F. (1961). The number concept: A phylogenetic review. Psychological
Bulletin, 58, 420-428.
Wolfe, J. B. & Kaplon, M. D. (1941). Effect of amount of reward and
consummative activity on learning in chickens. Journal of Comparative
Psychology, 31, 353-361.
Xia, L., Siemann, M. & Delius, J. D. (2000). Matching of numerical
symbols with number of responses by pigeons. Animal Cognition,
3, 35-43.
Zeier, H. (1966). Über sequentielles Lernen bei
Tauben, mit spezieller
Berücksichtigung des "Zähl"-Verhaltens. [About sequential learning
by pigeons, with special consideration of "counting" behavior.] Zeitschrift
für Tierpsychologie, 23, 161-189.
|
Acknowledgement
I would like to thank Li Xia, Martina Siemann, and Juan Delius, Universität
Konstanz, Germany,
for giving me pre-publication information about their research. I am especially
grateful to Martina Siemann for not only providing the summary of their
experiment but also for creating the figures demonstrating conditional
discrimination and cardinal responding. I also much appreciate Irene
Pepperberg's help in supplying the video clip of Alex. |
|


