IV.
A Prototypical Point Of View
According to prototype theory, categorization
is accomplished by the acquisition of a prototypical representation of
a category via a form of abstraction process. The prototypical representation
is assumed to be a summary representation that corresponds to the 'central
tendency', such as the arithmetic mean (Posner, 1969) or the mode (Neumann,
1977), of all the exemplars that have been experienced. New exemplars can
then be classified on the basis of their similarity to this 'best example'.
Consider, for example, what happens when one is asked to imagine a category
such as 'tree'. Usually a typical instance of this category is immediately
called to mind. The experimental investigation of this prototype effect
began with Attneave (1957), and lead to the prototype view becoming as
firmly established in the field of human cognitive psychology as exemplar
or feature theories (see Smith & Medin, 1981; Medin & Smith, 1984;
Homa, 1984, for a review).
In contrast, evidence in support
of the prototype theory is rather poor and contradictory in pigeons. While
the first attempts to demonstrate prototype effects produced negative results
(Pearce, 1989; Watanabe, 1988), more recent attempts yielded positive findings
(Aydin & Pearce, 1994; Huber & Lenz, 1996; White, Alsop & Williams,
1993). However, this does not warrant the conclusion that pigeons are able
to abstract prototypes. There is also little agreement concerning the specific
type of representation involved in prototypical categorization, and the
specific conditions that facilitate categorization. The common denominator
for all research in this field is a demonstration of the prototype effect.
The prototype effect refers to the fact that the prototype, or exemplars
that bear a close resemblance to it, are instantaneously classified. Sometimes
even more readily than those exemplars of the same category that have already
been experienced.
In an experiment, which we conducted
to investigate this issue (Huber & Lenz, 1996), our primary aim was
to determine what conditions facilitate prototype formation, rather than
to provide empirical support for the
 existence of some kind of abstract representation.
An examination of the tasks that have failed to elicit prototype formation
in pigeons suggests that category structure is crucial in determining whether
pigeons store associations with instances or features, or whether
they abstract prototypes. We adopted the classical "distortion rule" used
in human prototype experiments (e.g. Attneave, 1957; Fried & Holyoak,
1984; Homa & Chambliss, 1975; Posner & Keele, 1968) to obtain patterns
which varied around a prototype. For rules of this type, the prototype
represents a kind of average or central tendency of the distortions. In
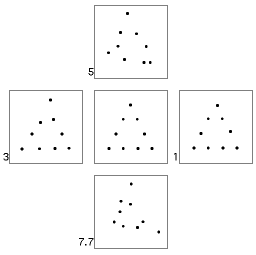
the archetypal experiment, Posner and Keele (1968) showed that humans readily
identify a prototype dot figure (a triangle)
underlying a series of distorted patterns of dots (in Figure 17 to the
left, numbers represent the level of distortion given in bits/dots). As
a result, the more similar a novel pattern was to a category prototype,
the easier it was to classify.
existence of some kind of abstract representation.
An examination of the tasks that have failed to elicit prototype formation
in pigeons suggests that category structure is crucial in determining whether
pigeons store associations with instances or features, or whether
they abstract prototypes. We adopted the classical "distortion rule" used
in human prototype experiments (e.g. Attneave, 1957; Fried & Holyoak,
1984; Homa & Chambliss, 1975; Posner & Keele, 1968) to obtain patterns
which varied around a prototype. For rules of this type, the prototype
represents a kind of average or central tendency of the distortions. In
the archetypal experiment, Posner and Keele (1968) showed that humans readily
identify a prototype dot figure (a triangle)
underlying a series of distorted patterns of dots (in Figure 17 to the
left, numbers represent the level of distortion given in bits/dots). As
a result, the more similar a novel pattern was to a category prototype,
the easier it was to classify.
Pigeons appear unable to abstract
prototypes in this manner. After having successfully discriminated triangular
patterns of dots, of a given distortion level, from arbitrary dot patterns,
the pigeons responded to a novel complete triangle less, rather than more,
vigorously (Watanabe, 1988). Note that this behavior can easily be described
as generalization from S+. Pearce (1989), who required pigeons to discriminate
between artificial polymorphous classes comprised of 'histogram patterns',
has provided further negative evidence. Three vertical bars, of varying
heights, were used as the defining feature dimensions, in that their combined
height defined their category membership. Pigeons that were trained on
patterns with the combined height of 15 and 9 were then tested with those
patterns that corresponded to the class average and patterns that corresponded
to the extremes of the short-tall continuum. In contrast to the predictions
of prototype theory, the pigeons' spontaneous classification of the extreme
patterns was superior to that of the prototype patterns.
The same pattern of results, namely
greater responding to extreme values than to any other instance along a
continuum from positive to negative classes, was also found in our faces
study (Huber & Lenz, 1993), and in von Fersen and Lea's (1990) study.
In principle, this pattern of results also corresponds to the 'super-releaser
effect' found in many classical ethological examinations of the sign
stimulus eliciting fixed-action patterns (e.g., Tinbergen, 1951). We have
interpreted this 'supernormal stimulus effect' in terms of feature learning,
rather than in terms of the acquisition of an abstract representation of
the category. However, those experiments, in which extreme values of the
underlying feature rule failed to evoke 'supernormal' classification behavior
(cf. Jitsumori, 1993; Lea & Harrison, 1978), have also failed to show
any signs of a prototype effect. Therefore, they have been more parsimoniously
explained in terms of learning about the entire patterns or some combination
of features.
We suggested that the abstraction
of prototypes is facilitated only when polymorphous stimulus classes are
composed of many similar stimuli that share a "point of departure" or origin,
but that cannot be separated in terms of the simple combination of feature
dimensions. We sought to design a prototypical categorization task that
fulfilled both of the following requirements:
-
There is no opportunity to discriminate
among classes by the adoption of a linear feature rule
-
Stimulus classes are very large so as
to impede exemplar memorization.
The first requirement can be satisfied
by designing stimulus classes that have features in common, but occupy
regions in a multidimensional stimulus space that are not linearly separable.
For instance, one cannot decide--as in the Huber and Lenz (1993) study--whether
a Brunswik face is positive by summing up the values of the eye, brow,
nose, and chin feature. The classes were designed using a distortion principle
and thus occupied highly overlapping regions in the multidimensional feature
space. Because the experimental design should favor the abstraction of
categorical information rather than learning individual instances by rote,
however, classification had to be facilitated on the basis of the central
tendency of the global stimulus distribution. In other words, correct classification
decisions should be determined not by reference to an undetermined number
of previously experienced training stimuli (exemplar view) but by reference
to the class prototype. A popular formulation of the latter strategy is
the "distance rule of classification" (Posner, 1969; but also see Reed,
1972). According to this rule, in our study (Huber & Lenz, 1996) the
criterion for class membership was the
differential similarity distance from the prototype (that I shall label
in geometric terms "radius"), measured by summing up the differences on
every feature dimension. Positive stimuli are equally similar and close
to  the prototype; negative stimuli are equally dissimilar and far
from it. If imagined in three-dimensional space, the stimulus classes might
be seen as hollow concentric spheres with different radius lengths around
a common center (Figure
18).Despite the typicality structure of the stimulus space, pattern
learning is still possible. Only a kind of trial-unique stimulus presentation
design (Bhatt et al., 1988; Wright et al., 1988), in which the repetition
of stimuli during training is minimized, is likely to inhibit pattern learning.
We, therefore, created a stimulus library that includes several thousands
of patterns. In order to enable the results of this experiment to be compared
with those of Huber & Lenz (1993), we used the same stimuli as in our
former study, but only increased the degree of variability.
the prototype; negative stimuli are equally dissimilar and far
from it. If imagined in three-dimensional space, the stimulus classes might
be seen as hollow concentric spheres with different radius lengths around
a common center (Figure
18).Despite the typicality structure of the stimulus space, pattern
learning is still possible. Only a kind of trial-unique stimulus presentation
design (Bhatt et al., 1988; Wright et al., 1988), in which the repetition
of stimuli during training is minimized, is likely to inhibit pattern learning.
We, therefore, created a stimulus library that includes several thousands
of patterns. In order to enable the results of this experiment to be compared
with those of Huber & Lenz (1993), we used the same stimuli as in our
former study, but only increased the degree of variability.
|
The distortion
rule to create two 'prototypical' categories
In Huber and Lenz (1993), each of
the features eye, brow, nose, chin of the Brunswik faces could take on
one of three values (-1, 0, +1). Here (Huber & Lenz, 1996), each feature
could take one of nine values (-4 to +4), and also differed on each dimension
in equal steps. This procedure generated 6561 (94) different patterns.
As in the classical prototype studies, the primary criterion for class
assignment was the similarity distance of a pattern from the prototype
(P) or, in the language of standard terminology, the distortion level.
Distortion levels were manipulated by varying the similarity distance between
sets of stimuli and a chosen prototype. Similarity distance was defined
by the additive combination of the difference between the values of all
four feature dimensions (a city block metric). For example, when comparing
a pattern containing the medium value on each dimension (i.e., 0, 0, 0,
0), with one containing extreme values (i.e., +4, -4, +4, -4), we obtain
the a priori overall similarity by summing the absolute difference between
each dimension (i.e., |4| + |4| + |4| + |4| = |16|). Using this 'transparent'
distortion procedure, we were able to specify 'distortion' according to
well-known feature dimensions, rather than by arbitrarily moving dots.
In other words, it was possible to compare two faces by finding that one
has, for example, a larger nose and more closely spaced eyes than the other,
rather than by comparing two arbitrary dot patterns. I will return to this
issue later when discussing our findings. |
The positive category (POS), in which
all stimuli were positively correlated with reinforcement, was defined
by a distance equal to 4 (according to our similarity measure, see sidebar).
The negative category (NEG), in which all stimuli were negatively correlated
with reward, was defined by a distance equal to12. As a result of selecting
two different patterns as prototypes, slightly different categorization
tasks emerged. For one group (the Prototype Identical Group, PIG), the
prototype was designated as 0, 0, 0, 0. If we average across all positive
stimuli shown in training (n=192), as well as across all negative stimuli
shown in training (n=528), the resulting arithmetic mean is identical for
both classes, namely again 0, 0, 0, 0. For the other group (the Prototype
Different Group, PDG), the prototype was designated as -2, +2, +2, -2.
As a consequence of the asymmetrical feature distribution in the second
group (a lower frequency of negative values for the features eye and chin
and a higher frequency of positive values for the features brow and nose),
averaging across the feature dimensions of all negative patterns shown
in training (n=607) resulted in an arithmetic mean that was slightly different
than that of the positive category (n=164). This enabled us to investigate
whether it is easier to divide classes on the additional information of
different prototypes than on the differing distance from a single prototype
alone.
Training involved the presentation
of arbitrarily chosen members of the two distortion levels. The implementation
of a random generator function in the program that created and presented
the faces permitted the use of a presentation order that was out of the
control of the experimenter. The difficulty of this task meant that the
training of the five pigeons lasted several months. Therefore, a high number
of the stimuli from each category (several hundreds) were shown to the
birds. The discrimination procedure used was in general the same as that
used by Huber and Lenz (1993).
In contrast to all the birds used
in the former study, only three of five pigeons achieved a satisfactory
discrimination level (r = 0.8) within 50 sessions of 40 trials each. The
two subjects that failed to solve the original classification task were
subjected to a single-negative condition involving a single negative pattern
rather than a negative class comprised of hundreds of patterns. This task
was quickly solved.
The most interesting part of this
experiment was the birds' performance during  generalization
tests, which involved patterns that varied according to their distance
from the prototype. Inspection of Figure
19 suggests the task to be a middle-value discrimination representing
a band of positive stimuli surrounded by a band of negative stimuli on
a single dimension. The most interesting question concerned the form of
the generalization slope at the stimulus region inside category POS. A
prototype effect (but also a peak shift effect, see below) would occur
if the slope continues to rise in the center of the distance dimension,
whereas orderly generalization around S+ would be found if the
generalization
tests, which involved patterns that varied according to their distance
from the prototype. Inspection of Figure
19 suggests the task to be a middle-value discrimination representing
a band of positive stimuli surrounded by a band of negative stimuli on
a single dimension. The most interesting question concerned the form of
the generalization slope at the stimulus region inside category POS. A
prototype effect (but also a peak shift effect, see below) would occur
if the slope continues to rise in the center of the distance dimension,
whereas orderly generalization around S+ would be found if the slope falls.
In Figure 20,
the peck rate to individual stimuli is plotted against their distance from
the prototype (radius). In contrast to the findings of Watanabe (1988),
stimuli positioned close to the prototype (marked in red) elicited even
more responses than the positive training stimuli at Radius 4. More generally,
according to the distance-from-prototype model, there is a significant
negative correlation between response rate and radius; the greater the
difference between the transfer stimuli and the prototype, the less frequently
the subjects pecked at the response key. This extremely orderly correlation
(Pearson product-moment correlations between -0.906 and -0.975) confirms
that a large proportion of the variance in pecking rate could be accounted
for by its linear relationship with the distance dimension.
slope falls.
In Figure 20,
the peck rate to individual stimuli is plotted against their distance from
the prototype (radius). In contrast to the findings of Watanabe (1988),
stimuli positioned close to the prototype (marked in red) elicited even
more responses than the positive training stimuli at Radius 4. More generally,
according to the distance-from-prototype model, there is a significant
negative correlation between response rate and radius; the greater the
difference between the transfer stimuli and the prototype, the less frequently
the subjects pecked at the response key. This extremely orderly correlation
(Pearson product-moment correlations between -0.906 and -0.975) confirms
that a large proportion of the variance in pecking rate could be accounted
for by its linear relationship with the distance dimension.
As in our former study, how strongly
the individual face features controlled classification performance merits
attention. This is particularly valuable with respect to the Prototype
Different Group. In this group, the different
prototypes to which the classes were anchored led t o the unequal distribution
of feature values across classes (see the colored bars in Figure
21). Consequently, there was a strong correlation between class membership
and attribute values. For example, a negative value for features 'e' and
'c' occurred approximately 1300 times in instances of the positive class,
whereas a positive value for these features occurred only about 50 times
as a signal for food. Simple linear feature rules, such as "if eye distance
is short then peck", would make category discrimination possible. By
and large, the combination of only two such feature rules would guarantee
significant (r>0.68) classification ability.
o the unequal distribution
of feature values across classes (see the colored bars in Figure
21). Consequently, there was a strong correlation between class membership
and attribute values. For example, a negative value for features 'e' and
'c' occurred approximately 1300 times in instances of the positive class,
whereas a positive value for these features occurred only about 50 times
as a signal for food. Simple linear feature rules, such as "if eye distance
is short then peck", would make category discrimination possible. By
and large, the combination of only two such feature rules would guarantee
significant (r>0.68) classification ability.
Control of the pigeons' pecking behavior
by independent features was examined by analyzing response rates
to stimuli as a function of their feature value (see the colored lines
in Figure 21).
As found in the previous study (Huber & Lenz, 1993), a linear feature
model predicts a linear relationship between response rate and feature
value, with extreme values eliciting both the highest and the lowest number
of pecks. In contrast, a prototype model would predict that responding
would be most pronounced in the presence of the prototypical feature attributes
(for Bird CG2 the values -2 and +2, respectively). Clearly, the data support
a prototype model rather than a feature model.
Interestingly, the pecking behavior
of the subjects that were successfully trained  with a single negative pattern (SNG) produced a different pattern of results
(Figure 22).
In contrast to the subjects of the Category Group, classification can be
best described in terms of a linear feature rule; responding was most pronounced
in the presence of the extreme (-4 and +4, respectively), rather than the
prototypical, values. These different findings alone confirm the importance
of considering category structure as an essential factor in categorization.
with a single negative pattern (SNG) produced a different pattern of results
(Figure 22).
In contrast to the subjects of the Category Group, classification can be
best described in terms of a linear feature rule; responding was most pronounced
in the presence of the extreme (-4 and +4, respectively), rather than the
prototypical, values. These different findings alone confirm the importance
of considering category structure as an essential factor in categorization.
In our original paper (Huber &
Lenz, 1996) we argued at some length that all three models of human categorization
could account for some part of the present findings. Let me summarize the
advantages and disadvantages of each theory.
A
Feature Account
The clearest evidence for feature
learning comes from the birds belonging to the Single Negative Group. A
linear feature mechanism of categorization easily accommodates their performance.
The birds learned to combine--in additive manner--the information from
all four feature dimensions until their judgments corresponded to a discriminant
function that accurately predicted class membership. The ease with which
these previously unsuccessful birds solved this task suggests that classes
separated by a linear discriminant function are easy to identify. The pattern
of responding shown by the remaining birds in this study also fits with
the basic tenets of feature theory. Classification behavior may be correlated,
not with the features as dimensions, but with the reinforcement rates of
their discrete values. In order to explain the bell-shaped generalization
functions around the prototypical feature attributes (see Figure
21) it is only necessary to consider that the prototypical feature
attributes on each dimension are those that have occurred most frequently
on reinforced trials, whereas the remote values on each dimension are correlated
with non-reinforcement. This explanation is not only consistent with the
Rescorla-Wagner (1972) theory, but also with frequency theories of feature
abstraction and concept learning in the human literature (e.g. Goldman
& Homa, 1977; Neuman, 1974).
An
Exemplar Account
As in the case of feature theory,
the amount of data that can be explained by the exemplar view depends upon
which version is applied. The simple notion that a novel stimulus is classified
on the basis of its degree of similarity to all stored training stimuli
is hard to defend, since the multidimensional average of the positive class
was either identical (PIG), or highly similar (PDG), to the average of
the negative class. This means that comparisons would balance out and the
classes would become indiscriminable. A modified exemplar view based on
Pearce's configural theory can also account for the present findings in
much the same way as it accounted for Aydin and Pearce's (1994) findings.
It rests on the possibility that an increased response rate to novel stimuli
near the positive prototype may be caused by decreased inhibitory generalization
from members of the nonreinforced category. The contrary effect, namely
a reduction in response frequency during novel stimuli more distant from
the prototype than the negative training patterns, may be caused by a loss
of excitatory generalization. Following Spence's (1937) theory of gradient
interaction, the prototype effect may be caused by a peak shift (Hanson,
1959; Purtle, 1973; Rilling, 1977).
The peak shift effects reported in
the literature, however, clearly indicate that the distance over which
the generalization peak shifts away from the S+ value, is rather short.
While it may be difficult to estimate whether the prototype value lies
within this distance, a negative peak shift is clearly absent. For both
birds, CG2 and CG6, the decreasing trend of response rates away from
S- (marked green in Figure
20) continued more than twice the distance between S- and S+ (marked
blue). Finally, the generalization gradients found in the present study
were quite different from the ones obtained by Watanabe (1988) in a similar
experiment. If generalization from stored S+ and S- exemplars is a general
classification strategy for pigeons, then why did Watanabe's pigeons not
demonstrate a steady response increase towards the prototype?
A
Prototype Account
A more coherent account of the transfer
performance of the three successful birds is offered by prototype theory.
We only need to propose the acquisition of a linear distance rule as a
predictor of class membership in order to explain the strong correlation
between distance from the standard pattern and response rate. Furthermore,
this model is the most parsimonious in terms of memory load and most economical
in terms of determining membership. A pigeon must keep in memory, for comparison
with a novel unseen exemplar, only the (single) representation of the central
tendency of the previously experienced class instances. In conclusion,
this dual classification mechanism will cope easily with large, open-ended
stimulus classes that show a polymorphous and typological (dense center--sparse
periphery) structure.
Next Section: A
Synthetic Approach Using Natural Stimulus Classes

