Visual Categorization in Pigeons

The term "feature" refers to any elementary property of a distal stimulus that is psychologically processed--an "atom of cognition". It is usually used to refer to the fixed properties of a stimulus, which are the most primitive or the lowest building blocks of object recognition and categorization (e.g. Bruner, Goodnow & Austin, 1956). Although the advantages of a feature learning over a template approach to categorization (e.g. Ullman, 1989) are already available in terms of straightforward models of similarity (e.g. Shepard, 1987; Blough, 2001) and of structured hierarchical representations, some would argue in favor of more flexible features (Steele, 1990; Schyns, Goldman & Thibaut, 1998). While a very large set of object descriptions and categories can be generated from a finite set of elements and combination rules, the fixed feature approach is limited to the possible combinations of the feature set.

Feature Analysis Versus Feature Learning

Feature analysis refers to the fact that a subject or species enters into a problem with a fixed set of features, to which it is sensitive. It will consequently fail the task if the categories to which it is exposed are not separable along these feature dimensions. If, furthermore, combinatorial power is also limited, then the animal will be required to classify objects in the natural environment by fixing on some specific, single feature. This ability is a natural example of a feature analysis system, and also exemplifies the power of such a simple strategy (Uexkuell, 1939; see also Herrnstein, 1985).

It is easy to imagine occasions on which features, not originally present in the system, are useful for distinguishing between important categories in the world that confront the organism (Schyns, Goldman & Thibaut, 1998). Feature learning would be able to tailor the animal's feature repertoire to the demands of categorization. The set of features used and/or the salience of these features could be continuously modified during the course of categorization. Such a flexible system would be able to adapt to a changing environment, especially in those situations in which it would be unrealistic to think that a system comes fully equipped to deal with them appropriately. Artificial tasks created in the laboratory provide a straightforward way of testing this ability.

A number of categorization experiments with animals that can be described in terms of feature theory have already been conducted. This is particularly apparent in those cases in which the task involved artificial stimuli devoid of the richness of natural scenes. Researchers have attempted to interpret these results by trying to identify those aspects that controlled the animals' classification performance. Such post-hoc analyses have been conducted either by correlating the feature values that the experimenter was attending to with the animals' response rates, or by submitting the data to more sophisticated statistical procedures, such as cluster analysis and multidimensional scaling (see Blough, 2001). The letters of the alphabet are stimuli that have been used repeatedly in such experiments (Blough, 1985; Lea and Ryan, 1983; Morgan, Fitch, Holman & Lea, 1976).

An even more illustrative example of artificial stimuli is the cartoons of the Peanut family used in the lab of Cerella (1980, see also Cerella, 1982, 1986). The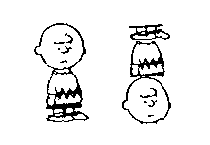

striking result of this frequently cited experiment, was the pigeons' resistance to deformations of "Charlie Brown" (Figure 10, see also Kirkpatrick, 2001). This finding is interesting because it is hard to reconcile it with our understanding of template action. If the animal is attending not to the entire figure, but only to some small component, then generalization should be preserved even if Charlie Brown is truncated, scrambled, or presented upside-down. A feature model need only assume that the local aspects of figures are processed separately and are position-invariant.

The strength of any feature model lies in its ability to explain virtually any categorization behavior, and in its plausibility in terms of informational economy. Furthermore, successful generalization can be explained in terms of common features and the associative strength that they acquire during training, rather than by evoking an obscure concept or straining the template account. If we accept that the presence or absence of a certain set of features is responsible for determining how a subject classifies an individual stimulus, then we need only specify how these features acquire their influence. If the total number of possible features belonging to separate classes of stimuli are predetermined, then one only has to specify whether responding has come under the control of these features. If this is the case, and a clearly specified feature model is able to describe the data adequately, then it would be superfluous to ascribe to pigeons the formation of a concept. Unsurprisingly, several experiments using this criterion have been successfully conducted (Jitsumori, 1993; Lea & Ryan, 1983; Fersen & Lea, 1990).

Following this line of analysis, even those experiments that have been described in terms of concept formation, might be explained in terms of feature-positive discrimination. For example, if pigeons receive trials in which photographs containing people signal food, and trials in which photographs without any people signal the absence of food. Then those features that are characteristic of people will steadily acquire associative strength due to their positive reinforcement history. In contrast, all irrelevant features, i.e. those that are present in both reinforced and non-reinforced trials, will acquire associative strength in an erratic manner and in the long term will lose attention. The problem with this approach, however, is that it cannot specify exactly what features are involved. The scarcity of information about the precise nature of the cues controlling the discrimination is endemic for categorization tasks involving complex stimulus classes (Cook et al., 1990; Fetterman, 1996). Inspection of the slides alone cannot allow us to determine which dimensions divide the feature space, especially when photographs of natural scenes are employed. Those experiments that employ slides of people, trees, bodies of water, fish, flowers etc are resistant to rigorous tests in terms of feature theory. This is not only true of the experimenter him- or herself, but also of the critical reader of such experiments who attempts to reevaluate the results but is not provided with the full set of pictures used (see Premack, 1983; Editor's comment: this should change with the increased use of the web as is evidenced many times in this volume).

One way of determining which aspects of a complex picture, or class of complex pictures, have acquired control over the subjects' responding is to analyze the subjects' misclassifications. Experimenters have sometimes found better performance on those slides that they would have classified as intermediate to poor with respect to the saliency of the underlying concept (Herrnstein & De Villiers, 1980; Schrier & Brady, 1987). This finding suggests that, in these experiments, the subjects' behavior may have been under the control of a slightly different concept to that intended by the experimenter. Analysis of those slides that elicited crude misidentifications, has proven to be especially informative, since it has evoked rather strong reservations about the conceptual ability of the subjects under investigation (e.g., D'Amato & Van Sant, 1988). D'Amato and Van Sant's (1988) monkeys, for example, showed persistent errors to those slides including patches of red coloration (e.g., a piece of watermelon in the center of a table). Such features are no doubt irrelevant from the point of view of the human concept holder, but not from the point of view of the monkey. The same control of animals' behavior by the background of photographs was also found in Green's (1983) reevaluation of Herrnstein's experiments, and in Honig and Stewart's (1988) experiment.

While it is clear that persistent reliance on the irrelevant features of a target concept is cause for serious concern about whether animals form concepts at all, it strongly supports the more parsimonious feature account. Animals do not learn about the defining features of a concept and neglect all other features that may be present, but are not necessary properties or characteristics of any member of the target concept. Rather they learn about any feature that occurs with some positive probability on trials and are followed by a specific psychological consequence (e.g. food).

As mentioned above, one severe problem with the feature account of natural categorization in animals is that the stimulus aspects controlling the subjects' behavior cannot be completely and reliably specified. One way to render this task more manageable is to use stimuli that are poor in detail and describable only in terms of a few well-understood features. The advantage of such an approach is two-fold. First, the number of stimulus aspects that might occur with a high probability can be reasonably reduced. For example, using line drawings can make a "hidden" feature such as a specific one-sided distribution of a hue or the amount of background (Schrier & Brady, 1987) unlikely to correlate with one stimulus class.

Second, the low-dimensional feature space of artificial stimuli enables the experimenter to arrange stimulus classes along a linear discriminant function (Nilsson, 1965). In terms of geometry, this means that the two categories to be discriminated by the animal occupy different areas in a multidimensional feature space. Such a clear-cut experimental design, that forces the subject to adopt the categorization rule or else fail, is achievable only if the stimuli are constructed by the experimenter.

More rigorous tests of the subjects' ability to extract the relevant features, and to combine them in a manner that most closely corresponds to the experimenter's categorization rule, requires a synthetic approach to categorization. This has been adopted with considerable success in Stephen Lea's laboratory in Exeter (Lea & Harrison, 1978; Lea, Lohmann & Ryan, 1993; Lea & Ryan, 1990; Fersen & Lea, 1990; see also the research of Shimp, Herbranson, & Fremouw, 2001) The synthetic approach is an a priori method that involves the construction of artificial concepts that can be defined by a small number of independent features, each of which comes with a predetermined probability of occurrence. One experiment designed according to all the above criteria was conducted as part of my Ph.D. thesis (Huber, 1991) and published thereafter (Huber & Lenz, 1993).

The two classes of stimuli used in this experiment could be distinguished on the basis of a "polymorphous feature rule". Ryle (1949) coined this term in order to describe the nature of ordinary language concepts. Wittgenstein (1953) argued, in a similar manner, that natural categories are ill-defined, i.e. they lack any singly necessary or jointly sufficient attributes of definition. More simply, the features of natural categories are not present in all exemplars, but are only characteristic or likely to be class properties. Consequently, the members of such categories do not have equal status, but are more or less typical of the category depending on the number of characteristic features that they possess. In order to approximate this philosophical account, and to make it manageable for psychological experiments, several researchers have used an "m-out-of-n rule" (Dennis, Hampton & Lea, 1973; Shepard, Hovland & Jenkins, 1961). According to this rule, membership information is a quantitative combination of several independent feature dimensions. Dennis, Hampton & Lea (1973), for example, asked students at the University of Cambridge to discriminate between artificial sets of stimuli that were defined by a two-out-of-three rule. Positive stimuli contained two out of possible three positive feature values, while negative stimuli contained two out of possible three negative feature values.

Lea and Harrison (1978), using a similar procedure for the first time with pigeons, reported successful training of the six training stimuli constructed using the above rule, and successful generalization to the two test stimuli (which contained all the positive or all the negative feature values). However, the very small number of training stimuli used in this experiment casts doubt upon whether the pigeons really learned about the features at all, or whether they just learned about the patterns in their entirety. Therefore, in my own experiments I used 62 stimuli, which I believed would increase the probability of feature learning. Simple line drawings were created that resembled, to the human observer, human faces (called "Brunswik faces"). Three examples of these patterns are depicted below (Figure 11).

Egon Brunswik originally used these types of stimuli in an investigation of human

expressions (Brunswik & Reiter, 1937). Many years later, Reed (1972) used them to investigate human visual categorization. We created them on the computer and presented them on black-and-white slides with luminous contours and dark backgrounds. The schematic faces consisted of four facial features that could be assigned one of three values. The four facial features were distance between the eyes (e), height of the forehead (brow, b), length of the nose (n), and position of the mouth (chin, c). All four features were assigned values of -1, 0, or +1 (arbitrary values that correspond to equally large displacements). Using this method, it is possible to generate 81 (3⁴) different faces. The next step involved the arbitrary assignment of the feature values to the categories. The pattern containing a short distance between the eyes, a high brow (a low eye position), a short nose, and a high chin (a high mouth position) was designated as the prototypical negative pattern [e-b-n-c-] (left figure); while the pattern containing a wide distance between the eyes, a small brow (a high eye position), a long nose, and a small chin (a low mouth position) was designated as the prototypical positive pattern [e+b+n+c+] (right figure). The intermediate figure is depicted in the center.

According to the m-out-of-n principle, the categorization rule can be defined as the quantitative combination (or sum) of feature values, plus a threshold criterion that separates the two categories. By this definition, each pattern with a negative feature sum (n=31) belongs to one category (NEG), while each pattern with a positive feature sum (n=31) belongs to the other category (POS). (The 19 patterns with a feat

ure sum of zero were omitted from the experiment.) Inspection of these stimuli (Figure 12) reveals that no single feature dimension alone is a perfectly reliable cue, but has an equal, low value of membership predictability. In other words, attending to eye distance alone can never provide sufficient information to determine trial outcome. The same is also true of the feature values. Negative values are correlated with category NEG and positive values with category POS, but only weakly (p = 0.55). Furthermore, even the opposite value (negative for category POS, and positive for category NEG) occurs occasionally (p = 0.13). Finally, feature values of zero occur equally often in both categories (p = 0.32).

As predicted by Wittgenstein and Ryle, the instances of a polymorphous class are not equally valid members of the categories to which they belong. Typicality of category membership varies along the summary dimension; one pattern in each class (with an absolute feature sum of four) is a perfect category member, patterns with an absolute sum of three are very typical, those with an absolute sum of two are intermediate, and those with an absolute sum of one are poor members.

Therefore, the only way to classify the stimuli exactly is to respond to their "feature summary". In order for successful categorization to occur we predicted that the pigeons must be able to:

Based on these predictions, the model was supported in two ways. Pigeons were trained on all 62 stimuli, but in a stepwise manner in order to investigate how stimuli introduced at later stages are classified (a form of generalization test). Afterwards, several independent observers assessed the veridicality of the above criteria, i.e. whether selective attention to specific facial features varied, and whether the features were combined additively or in a more integrative manner.

The pigeons' learning performance was surprisingly good. After only three weeks of training, which consisted of three stages that involved an increasing number of stimuli (first 10, then 20, and finally 60), the three experimental subjects were able to perfectly divide all stimuli into the categories defined by the experimenter. Inspection of the learning curves (Figure 13) reveals that some disruption occurred following the shift from the first to the second training stage. However, the fact that these errors occurred with an equal frequency during the presentation of the already known stimuli and the novel ones, led us to reject pattern learning effects. From session 13 onwards, when the number of training stimuli was increased from 20 to 60, we found highly accurate initial responses to novel stimuli. Both birds that continued discriminating (unfortunately pigeon, st3, died) demonstrated almost perfect categorization abilities. The discrimination ratios for these two birds, averaged across sessions 15 - 19, were 0.96 and 0.98. This was achieved by pecking between 2.0 - 3.6 times more frequently to positive stimuli than to negative ones.

Even more informative than the learning performance of the birds, was the analysis of the pecking rates directed at individual instances of the categories. According to prediction 1), all four facial features should have exerted equal control over the birds' responding. To test this prediction we applied a method already used by Lea and Ryan (1983). Pecking rates to all 60 stimuli (i.e., mean number of pecks to each stimulus across all sessions of stage 3) were subjected to a multi-factor analysis of variance, conducted for each bird separately. This confirmed that all features had a significant effect on the variance of pecks across stimuli.

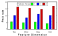ccording to prediction 2) the birds should have paid equal attention to all four features, i.e. pecking to the features presented with the same attributes should have been equivalent. It can be seen that plotting the distribution of pecking rates as a function of feature value during the third training stage (Figure 14) fulfilled this criterion.

Finally, according to prediction 3), combining the feature values in an additive manner should produce an orderly relationship between the sum of the feature values of a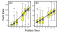

particular face and the rate of responding that it elicited. Although not achieved in every instance, when we averaged across all stimuli we found a remarkably orderly correlation between pecking rate and feature sum (Figure 15), sufficient to support a linear feature model (see sidebar below).

A quantitative examination of the pigeons' classification behavior

One feature of these results is that they can easily be interpreted in terms of learning theory. Consider, for example, one well-known feature model of discrimination. The Rescorla-Wagner (1972) model predicts that each feature value will gain positive associative strength during the course of learning, to the extent that it occurs on positive trials, and vice versa for feature values occurring on negative trials. We saw earlier that the positive feature value (+1) is correlated with positive patterns, and that the negative feature value (-1) is correlated with negative ones. Hence, while positive features will acquire positive associative strength, negative features will acquire negative associative strength. Because this model is a form of independent cue model (Reed, 1972), the strength of responding during presentation of a compound stimulus is determined by a linear combination (sum) of the associative strengths of its components.

An attempt to quantitatively describe the classification performance of the experimental subjects is involved in Huber and Lenz (1993). The R²-values of the multiple regression functions that involved the four predictor variables (i.e., the values of the four feature dimensions) exceed, for both birds, the 80% level. By direct application of the variable weighted linear feature model (Lea & Ryan, 1990), we can describe the discrimination behavior of the two pigeons by means of a simple linear equation:

pecks = k + b1e + b2b + b3n + b4c.

k is a constant for pecking; e, b, n, and c are the feature values; and b1-b4 are the weightings of the feature dimensions. A multiple regression analysis of the data from Bird st1 yield the following equation:

pecks_(st1) = 10.69 + 3.17e + 3.51b + 3.26n + 4.97c

For Bird ht1 the equation reads:

pecks_(ht1) = 8.8 + 1.66e + 2.23b + 1.64n + 1.95c.

However, this may not be the whole story. Although it may seem like I am splitting hairs, the factor responsible for the remaining proportion of variance in the pigeons' responding remains to be identified. Look at the following modified Figure 15 in the next figure (see Figure 16). Especially for Bird ht1 it is easy to recognize that the six points representing pecking rate as a function of feature sum are not located precisely on the regression line. If we combine the three points of each category, then a more or less sharp crack appears. It would appear that the pigeons have gathered additional information in order to divide the class even more efficiently than would have been possible if only the summary information was being used. Statistical evidence for this assumption can be obtained by inserting an additional factor into the multiple regression analysis with the value of one for positive stimuli and zero for negative ones (see also Lea & Ryan, 1983). For one pigeon (ht1), this additional independent variable that we may call the "category variable" accounted for a significant proportion of the variance in pecking frequency.

What exactly is the source of the additional information that the birds were using? One possibility that we have considered is the use of Gestalt information, extracted from any relationships between the four facial features. However, the analysis of variance revealed that there was no interaction between the facial features. Therefore, another possibility is that learning about the specific configurations of the exemplars contaminated feature learning. This is not implausible if one considers that some faces, particularly those already presented during the first and second training stages, were shown up to 53 times. The fact that the other pigeons' performance was only marginally affected by the additional information led us to continue interpreting the results of this experiment in terms of a feature account.

Some authors are not so confident. One particularly interesting explanation of our results is in terms of configural theory (e.g. Pearce, 1987, 1994). According to configural theory, which is an alternative to an elemental theory of conditioning, "if a compound stimulus is presented for conditioning, discrimination of categorization, then a configural representation will be formed of the entire pattern of stimulation. This representation will then enter into a single association with the outcome of the trial" (Pearce, 1997, p. 116). The important point of this statement is that generalization to novel stimuli occurs, not along separate feature dimensions, but along the distance dimension on which configurations of stimuli, rather than their feature values, are located. Applied to categorization problems, stimuli that are repeatedly paired with food during training will acquire positive associative strength, and this excitation will generalize to any other similar stimuli presented for the first time during a transfer test. The same is also true of negative training stimuli; i.e. inhibition will generalize to other similar test stimuli. "The interaction of these sources of excitation and inhibition will leave the new stimulus with a net level of excitation, and it will elicit a response appropriate to the category to which it belongs" (Pearce, 1997, p. 122).

It is not difficult to recognize that there is a close relationship between the configural theory of conditioning and the exemplar view of categorization. In fact, generalization from stored intact stimulus compounds during transfer tests has been proposed not only by Pearce and collaborators (e.g. Pearce, 1988, 1989, 1991; Aydin & Pearce, 1994), but also by Astley & Wasserman (1992). Whether this theory has any relevance for the results reported above remains to be specified. At first sight, the remarkable difference in responding to members of the same category, (e.g. to members with an absolute sum of three, and to members with an absolute sum of one), might seem incompatible with the exemplar view. However, as Pearce (1997) has convincingly argued, faces with a net sum of +1 are much more similar to faces with a net sum of-1, than to faces with a net sum of +3. Hence inhibition will be more likely to generalize to these negative stimuli. Faster responding to a +3 face is therefore a result of peak shift effects (see also Spence's (1937) theory of discrimination learning).

As this simple experiment involving three pigeons categorizing Brunswik faces has demonstrated, it is rather difficult to disentangle feature theories from exemplar theories in terms of the general predictions that they make. Despite this difficulty, I attempted such an endeavor by presenting a specific test stimulus during categorization training.

The two theories make radically different predictions about responding to this test stimulus. The test, which followed the rationale of Medin & Schaffer (1978), was intended to provide support for context theory (the first formal application of the exemplar theory). Immediately after the second training phase, five test sessions were administered that consisted of the presentation of the training stimuli from the second training phase. However, one specific test stimulus was presented twice

Stimulus "26" was presented 10 times and followed by a neutral trial outcome: the termination of the trial after 10 sec. The average number of pecks elicited by this "ambiguous" pattern was 2.80, 3.00, and 3.25 for Birds ht1, st1, and st3 respectively. Pecking during the presentation of the comparison stimulus "64" varied between 11.25 and 13.50. Furthermore, there was no single case during all five test sessions, in which a positive stimulus elicited fewer than 10 pecks (pecking to negative stimuli varied between one and 10 pecks). Therefore, it would appear that all three pigeons recognized Face "26" as signaling the absence of food--a finding which is in full accordance with feature theory, but in sharp contrast to the predictions of the exemplar view.

Unsurprisingly, researchers that favor an exemplar account of categorization over a feature learning account, will not be sufficiently convinced by this single finding. It is admittedly difficult to derive any firm conclusions concerning the relative merits of exemplar and feature theory. Instead of training legions of pigeons in order to test different versions of the available theories, we can change to a radically different approach.

Computer simulations based on connectionist or neural networks (e.g. Gluck and Bower, 1988; Gluck, 1991; Shanks, 1991) have proven to be particularly useful in this respect. Given that both elemental and configural theories are already available in the form of computer models, we only have to feed our data into the different variants. Because the data from three pigeons seemed to be rather poor for such modeling, Renate Lenz trained three further pigeons on the original task. The models were then compared by feeding into the computer the stimuli (or their respective feature values) in exactly the same order as they were presented to the pigeons during the various training stages.

Before evaluating the main results of these simulations, it is worth noting that the performance of the five pigeons used in these simulations varied in two respects. First with respect to selective attention during the early training phases, and second with respect to learning speed. Consequently, the degree of fit of the various models depends on which subjects were being compared. More specifically, in all those variants of the models in which we included a variable for selective attention, the proportion of variance accounted for differed considerably. In order to examine the data in more detail, they were subjected to linear regression analyses, using several different combinations of the predictor variables.

A summary of the percentage of variance explained by the linear regression analyses of the predictions of the different models, together with the empirical data for each bird is shown in Table 1. The original version of the configural cue model does not account for selective attention. If the pure version of this model is compared with the predictions of a feature model, which does not include selective attention, and feature sum is used as a predictor of pecking behavior, then a considerable difference is found for fast and slow learning pigeons. In the case of the two fastest learners (the first two subjects), the feature sum explains the data significantly better than the configural cue model. In the case of the two slowest learners, it is the other way round.

When individual attention weights were included in the configural cue model, the comparison revealed that the variably weighted linear feature model, represented here as multiple regression analysis, is superior for all the fastest learning birds (P1, P2, P3). The variably weighted linear feature model also revealed better results for Bird P4. Only for Bird P5, were both models equally good predictors. However, the predictions of the configural cue model can be further improved by assuming a higher degree of similarity between the stimuli. This is true especially in the case of fastest learners P1, P2 and P3. Nevertheless, for P1 and P3, the variably weighted linear feature model still showed better results. For the slow learners, P4 and P5, this modification provided no improvement. Finally, in order to extend the generality of our findings, we added a further exemplar model. However, using Kruschke's neuronal network model ALCOVE (Kruschke 1992), we failed to make any further improvements.

In summary, for all pigeons, the variably weighted linear feature model explained the greatest percentage of variance. Nevertheless, there are ways in which the predictions of the configural cue model could be improved, such that for some pigeons (P2, P4 and P5) the difference was no longer significant. However, the predictions of the variably weighted linear feature model can also be further improved for P2 by including additional variables (e.g., a dummy variable and a variable that represents the frequency of pattern presentation of the individual stimuli) in the multiple regression analysis. The fact that for the fast learners (P1, P2 and P3), the variably weighted linear feature model shows better results than the configural cue model, indicates that some sort of feature extraction mechanism was involved. However, there might still be ways in which to improve the predictions of the configural cue model for individual pigeons (Pearce, 1994). At this point, however, we do not know of any straightforward way in which to do so.

In conclusion, we may ask what advantages can be gained by having two models converging, if the models are simulated by computers in which the boundaries between the theories dissolve in the net of (hidden) units. For example, it is questionable as to whether an exemplar model is turned into a feature model by implicitly using individual feature weightings for representing the stimuli. Furthermore, there is little agreement concerning how similarity can be correctly assessed, how many entire patterns enter into associations, and how reliably the models can be extended to include natural stimuli. Computing similarity in terms of common elements may seem, at first, to be relatively straightforward. It is, nevertheless, unclear as to what should be regarded as an element, even for simple stimuli such as Brunswik faces. Natural stimuli cannot be seriously simulated in terms of A+ B+ AB-. If, however, they could be reduced in this radical way, then we are in the midst of the feature theory. On the other hand, proposing that features are not perceived and are processed independently, is by no means an objection to feature theory but only to one traditional, perhaps out-of-date, version.

Further progress must be made in order to clarify these points. For the present, however, we may agree with Pearce (1997) "that the mechanisms that are believed to be responsible for the way animals solve relatively simple discriminations are also likely to be responsible for the way they solve complex categorization problems."

Continuing to improve the feature account of categorization requires that we consider how natural categories are distributed over the feature space. In our experiment, the categories consisted of many exemplars, which differed only in terms of a few stimulus dimensions. The decomposition of these patterns into stimulus components should thus have been fairly easy and economical. Moreover, the separability of the feature dimensions in the case of the Brunswik faces should have facilitated this decomposition. It is likely that, integrative dimensions will be processed by the visual system in substantially different ways. Finally, the fact that no single cue or feature alone was sufficient for differentiating between the categories would have favored a strategy that combined information from several feature dimensions in order to solve the classification problem.

If we adopt this point of view, then it is fair to admit that the above findings cannot be generalized limitlessly. From the literature on animal concept discrimination, and from our own data, it is possible to derive at least three important constraints on the use of this strategy:

A few years ago, Lea, Lohmann & Ryan (1993) reported an experiment in which pigeons were confronted with stylized monochrome drawings that consisted of five relevant feature dimensions. Although this experiment was similar to ours in many respects, the pigeons experienced considerable difficulty when spontaneously abstracting these equally balanced features. Although pigeons may be able to attend to these features when forced to do so, there may be a limit to the number of features that can simultaneously control behavior. If too many features are relevant for the concept rule, then the animal may attend to only a subset of the relevant features, especially if they are very salient. The failure of dominant features to control behavior may prevent accurate classifications from being made. Support for this can be found in an experiment with "faked pigeons" (Lea & Ryan, 1990), in which wing feature was found to control the classification performance of the birds much more so than any of the other relevant features. However, despite these occasional problems, feature learning is not an unreasonable model of categorization. Fersen and Lea (1990) and Jitsumori and Yoshihara (1997), for example, showed that pigeons are more than capable of attending to five mutually orthogonal features simultaneously, and categorizing successfully despite considerable differences in the salience of the relevant feature dimensions.Because I will discuss the difficult and important aspect of 'naturalness' in Section V, it may suffice here to introduce this aspect by referring to an informative experiment in this respect (Click here to see material on Fersen & Lea, 1990).

The third factor that is believed to interfere with category learning is the structure of the similarity space. As we ourselves have admitted (Huber & Lenz, 1993), the application of an m-out-of-n rule for category definition, leads to a similarity structure that may not be representative of natural situations. Since the four feature dimensions we used did not correlate with one another, a rather "flat" structure emerged, with no single stimulus rising above the others. Moreover, the classes did not deviate from one another to occupy distant regions in the similarity space. For example, in our experiment each category consisted of 16 stimuli with an absolute sum of one and 15 with an absolute sum of greater than one. It is possible that the omission of those 19 patterns with a feature sum of zero might have facilitated category discrimination, as proposed by Lea, Lohman and Ryan (1993). I doubt whether our Brunswik classes represent genuine clusters of relatively similar stimuli.

In more natural situations, ambiguous category exemplars located near to the category border are much less frequent. To put it more pictorially, natural categories represent mountain landscapes, with dense regions around class centers and sparse regions near the boundaries. The reason for this kind of unequal distribution in the similarity space is the high correlation between features that are class-typical. Trees, for example, vary considerably, but some features such as green and leaf, occur together. This "nested" feature distribution has been nicely illustrated in an experiment by Jitsumori (1993) in which pigeons were shown to attend strongly to specific combinations of features. In the same line of argument, within-compound associations were proposed to be important in conditioning experiments to simplify the task (cf. McLaren, Kaye & Mackintosh, 1989).