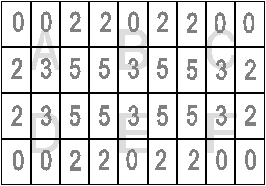Appendix A: Cognitive Map Memory Size
The use of a
hierarchical cognitive map to represent an environment with N
places, reduces the number of connection values in a
nonhierarchical map to a considerable smaller number (see Voicu
& Schmajuk, 2001b). Figure 1B
illustrates a canvas for an environment subdivided in N (36)
places, and
Figure 3
illustrates how the environment is represented in a
nonhierarchical cognitive map. The cognitive map represents all
the connections between a given place in the environment with
all other possible places. Because the connection of a place
with itself (always equal to 1) is not stored in the map, the
number of connections equals N2 - N. That is 1260
connections for an environment with 36 places.
Assuming a WM
capacity W = 6, then the number of levels needed to represent
this environment is given by L = log N/ log W = log 36 / log 6 =
2.
Figure 4
shows how the original environment is represented in a
hierarchical cognitive map in which the canvas is subdivided in
6 regions with n (6) places each. Now, instead of representing
all the connections between a given place with all other
possible places in the environment, we represent the connections
(a) between all places in a region plus the connections (b)
between places at the borders of that region with those places
in neighboring regions that are adjacent to them.
If n (6) is the
number of regions, the number of places in a region is N/n (6),
and the number of connections between places inside the region
is (N/n)2 - N/n. That is, for an environment with N
(36) places, subdivided in n (6) regions, the number of
connections is 30 in each region. The number of connections at
the borders between regions is calculated as follows. The 4
places located at each corner of a region have 5 connections to
places located in neighboring regions (see Figure A1),
thus the total number of corner connections is 20. Non-corner
places located at the borders of a region have only 3
connections, thus the total number of non-corner connections for
a region with 6 places is given by the number of non-corner
places (6 – 4 = 2) multiplied by 3, i.e., 6. Therefore, the
total number of connections at the borders of a region with 6
places surrounded by other regions of the same size is 26.
Therefore, the total number of connections for the lower level
is given by [(N/n)2 - N/n]
´ n + 26
´ n = 180 + 156 = 336.
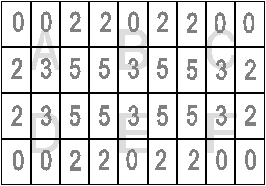 |
Figure A1.
Numbers represent the number of connections from a
place in one region to adjacent places in other
regions.
|
Once the number of
connections at the lower level have been calculated, we go to
the second level and represent the connection between regions.
Applying the same rule we applied before, this number is n2
- n. For n (6) regions, the number of connections for the second
level is 30.
Finally, we need to
connect the representation of each region in the second level
with their respective places in the first level (see
Figure 4). For n
(6) with N/n (6) that is 36 connections. Therefore, the total
number of connections in the hierarchical map is 336 + 30 + 36 =
402, much smaller than the 1260 connections needed to represent
the same environment in a nonhierarchical cognitive map.
However, as shown in Figure A1,
no region in this environment is surrounded by other regions,
and therefore, the number of connections (b) at the borders of a
region is smaller. This number is 82 for the environment
represented in Figure A1. The
total number of connections in this case is 328.