"Generalization within classes and discrimination between classes - this is the essence of concepts"(Keller & Schoenfeld, 1950, p. 155).

II. Exemplar View 

The universality and simplicity of generalization and discrimination has led many theorists to the most elementary level of categorization, i.e. behavioral analysis (e.g. Wasserman & Astley, 1994). According to behavioral analysis, which is based on the principles of conditioning, classes represent sets of stimuli with identical functions. These sets of stimuli are unified, not by a rule, a common feature, or an abstract representation, but by a common psychologically significant consequence (Skinner 1935). In the terminology of human categorization theorists, exemplar models predict categorization in such a manner.

Exemplar models are the most parsimonious models of categorization in terms of the underlying associative mechanism (see Chase & Heinemann (2001) for more on exemplar models and an actual working example). Proponents of exemplar models assume that intact stimuli are stored in memory, and that classification or recognition is determined by the degree of similarity between a stimulus and the stored exemplars. Simple generalization effects explain correct classification of novel (previously unseen) instances of categories. The tendency to respond to instances to which an individual has already been exposed will generalize to a similar, novel stimulus when it is first presented. This means that only the item information is used for classification decisions, and that categorization relies on the comparison of a new stimulus with known exemplars of the category. Therefore, generalization gradients have to be anchored to individual stimuli, and the individual exemplars have to maintain their memorial integrity even if the number of experiences relevant to a category is increased dramatically.

There are, however, a number of problems with the exemplar theory of categorization. Proponents of such theories cannot agree as to: a) how many exemplars can be stored or retrieved for comparison, and b) how similarity can be computed so as to ensure that responding generalizes only to those instances of the same category. The first problem is not only a matter of memory capacity, but also of feasibility. Categorization, according to exemplar based processing, is determined by the number of exemplars to be remembered. "Therefore, any exemplar model which assumes that all experienced exemplars are remembered may not apply to pigeon categorization when birds are trained with large numbers of non-repeating stimuli" (Bhatt et al., 1988). This criticism of the exemplar model can be overcome by assuming that categorization is based on a small subset of the total number of stimuli, or that specific retrieval rules act to determine which patterns are most likely to be accessed. The same is also true of novel stimuli presented in a generalization test. The average distance model (Reed, 1972), for example, assumes that the classification process involves the computation of similarity distances between the new pattern and all known members of a category. According to this extreme variant of the exemplar model of categorization, the subject stores all experienced patterns in memory, and retrieves information when a new pattern has to be classified. Some exemplar models do, however, allow for more abstract representations (e.g., Medin & Schaffer's context theory, 1978).

One may question the relevance of artificial tasks for natural categorization. Learning about perceptual classes in nature by recognizing every instance may sound like an impossible feat, but it has to be taken seriously. Although the number of possible pictures of "a tree" or "not a tree" is infinite, the actual number used in any particular experiment is likely to be finite. A series of experiments reported by Vaughan and Greene (1984), for example, revealed that the pigeon has quite striking powers of exemplar learning and retention. In these frequently cited experiments, eighty pictures of outdoor scenes were arbitrarily divided into two categories, positive and negative, and shown to three pigeons daily in different sequences. The only way in which performance on this task could have improved would be if each pigeon memorized whether each exemplar was positive or negative, since there was neither a concept nor a feature rule that distinguished the two categories. Against the odds, the pigeons were not only able to sort the 80 pictures correctly (with a probability of discriminating by pure chance well beyond 10-10), but they also learned to respond correctly to no less than 320 such pictures.

Fersen and Delius (1989) subsequently obtained even more outstanding results. Their pigeons were capable of discriminating 100 different positive stimuli from a further 625 similar negative stimuli. Tests conducted with novel stimuli indicated that the birds had not only memorized the positive stimuli, but also the negative ones. Furthermore, the birds retained this information over a period of several months, supporting the view that persistent and capacious memories are not restricted to food-storing animals, but may reflect a fitness advantage accruing from extensive and thorough knowledge of the environment.

Given the remarkable capacity of pigeons for learning specific exemplars, some researchers may tend to judge it as a sign of dullness, rather than of intelligence. The ability to learn relational or abstract concepts is more likely to provide evidence of intelligence. Throughout this chapter, however, I will argue for the need to be cautious in this respect. Greene (1983) provides an illustrative example of the overestimation of the pigeon's spontaneous discriminative abilities. Greene trained pigeons to discriminate between slides on the basis of a "repetition" concept. However, those birds actually mastered the task by responding to minute differences between the two "copies" of the slides. In the following section, I will offer yet another example of exceptional exemplar recognition by pigeons that were originally trained on an abstract concept. In this example, the pigeons were required to discriminate between different "chess-board patterns" according to the presence or absence of vertical symmetry.

Learning By Rote Instead of Abstracting A Symmetry Concept

The data presented in this section are from a long-term study of symmetry recognition that involved several stages and variants (Huber et al., 1999). However, I will confine my report to a single experiment that provides ample evidence of the pigeons' ability to switch from learning about the experimenter's abstract  class rule to learning about the more congenial instances. We used in this, and in all following experiments, members of the lively and robust "Strasser" strain of pigeon.  A total of 16 subjects were trained to discriminate a set of 20 vertically symmetrical chessboard-patterns (assigned as "positives" for one group, and as "negatives" for the other group) from a set of 20 patterns without a symmetrical axis (with the reverse contingencies).

We used two different types of black-and-white chessboard patterns in order to test certain models of symmetry recognition. One type (the "COMPACT" pattern) consisted of a vertical axis with "whiskers" on both sides. In the case of the symmetrical pattern, the whiskers on one side of the vertical axis were a mirror image of the whiskers on the other side.  In the case of the asymmetrical pattern, the whiskers were randomly distributed across both sides of the axis (Figure 3). The outer contours of all the figures were filled black. The exemplars of the second type of pattern (the "SCATTERED" pattern) were much more like chessboard patterns; i.e. the small elements were scattered across a 6x6 matrix (Figure 4). However, it would detract from the main point of this study if the differences between these two types of stimuli with respect to the assessment of symmetry were discussed more thoroughly. Only the striking difference between the learning curves of the two experimental groups warrants mentioning this difference. 

Members of the stimulus classes appeared, one at a time, on a computer monitor close behind a transparent pecking-key. The pigeons were required to peck frequently when a positive stimulus appeared in order to obtain food, and to suppress pecking when a negative stimulus appeared in order to terminate a non-reinforced trial. This type of go/no-go procedure (see details in Figure 5 below) was first used in Herrnstein's laboratory (Herrnstein et al, 1976; Herrnstein, 1979; Vaughan & Greene, 1984) and has also been repeatedly employed in our own laboratory.  

Figure 5: The go/no-go successive discrimination procedure A standard training session--which is administered once a day, five times a week--consists of 40 trials (elementary training unit). At the beginning of a trial a stimulus is presented directly behind the pecking key. During the first 10 s of a trial, pecks emitted onto the response key are counted but have no scheduled consequences. Only these responses enter into the data analysis. Following this 10-s period, and a further 10-s variable interval (VI) with a range of 1-20 s, subjects enter the consequential phase of the experiment. If the stimulus is positive, the first response to occur within 2 s of the previous response results in reinforcement being made available for a 3-s duration. If a negative stimulus is presented, the trial is terminated if the pigeon is withholds pecking for 8 sec during the consequential phase. If, however, the bird pecks continuously during the presentation of the negative picture, following the timing-out of the VI schedule, the picture presentation remains active. After trial termination, an inter-trial-interval (ITI) of 3 s follows, during which time the monitor is dark. The sequence of positive and negative trials follows a pseudo-random schedule. No more than 4 positive or 3 negative trials can occur in a row and the first trial is always positive.

If pigeons learn, this procedure results in a high rate of responding to patterns identified as positive, and a low or zero-rate of responding to patterns identified as negative. In trials pigeons are uncertain as to what group a stimulus belongs, they peck at an intermediate rate. Learning speed and accuracy are measured using Herrnstein's rank-order statistic, rho.

Plotting the learning curves of the two 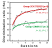groups in a single figure (Figure 6) reveals a surprising pattern of results. The investigation of symmetry conceptualization was overshadowed by a strong effect of stimulus type. Pigeons that were presented with the compact patterns experienced considerable difficulty when discriminating between symmetrical and asymmetrical stimuli. On the other hand, pigeons presented with the scattered figures showed substantial discriminative abilities. This result is surprising mainly with respect to the abstraction of the symmetry rule. If this rule is nothing more than a logical device, then no difference between the types of stimuli should have occurred. For example, humans informed about the underlying concept would have no difficulty in sorting the figures in both cases. If its acquisition, however, is bound to particular visual aspects of the figures, as many pattern recognition theories suggest (e.g. Osorio, 1996), then one may wonder whether we should continue to speak about abstract concepts at all. In any case, generalization tests involving the presentation of novel stimuli should allow us to determine whether the successful subjects learned the task solely by memorizing the specific training exemplars.

Such an endeavor requires the presentation of specifically selected test patterns, rather than the presentation of previously unseen instances of the training sets. In principle, the ability to capitalize on abstract relations, such as symmetry, can expand the class boundary by an unlimited amount, since boundaries will no longer be restricted by absolute class characteristics. Virtually any picture or object that is bilaterally symmetrical should be correctly classified when it is first encountered. Generalization then becomes a matter of inference, rather than of perceptual similarity. If, on the other hand, common features are involved, then transfer should occur along this dimension. Generalization will then become a matter of similarity. Finally, learning the training stimuli by rote in a photographic, integrative manner should severely impair generalization performance. Even minute changes in the idiosyncratic structure of memorized stimuli should result in a sharp trade-off. Generalization should then become a matter of indiscriminability.

In the type of transfer tests that we have chosen, we were able to determine the pigeons' categorization strategy from their unforced choice of novel stimuli, which were selected because of their similarity to the training patterns. In the first transfer test we simply used novel exemplars from homologous sets. Twenty novel compact figures and 20 novel scattered ones were interspersed in further training sessions  (see stimuli in Figure 7). We then examined whether transfer was limited to the training set by exchanging the test stimuli, e.g. showing the COMPACT group the scattered figures and vice versa. A negative result here would imply that transfer was dependent on absolute class characteristics. Even if the pigeons did master the transfer test, it would not provide unequivocal evidence of the possession of a pure abstract symmetry concept. Therefore, a more precise assessment of whether performance was contaminated by remembered stimulus aspects was sought using a final test that involved modified training patterns (see stimuli in Figure 8). For each group, we modified five symmetrical training patterns in six steps; three of which generated asymmetric patterns. These steps corresponded to various amounts of change  (either two, four, or six square elements have been displaced, omitted, or added). Thus, transfer behavior could vary according to either a) degree of symmetry, or b) amount of change. If it were found that the birds were influenced by a), then this would provide evidence of symmetry conceptualization. Whereas an effect of b) would indicate that transfer was the result of similarity to memorized training patterns.

The first two tests, which involved the presentation of test stimuli from the birds' own training class as well as from a foreign training class, revealed that only among the successful birds of Group SCATTER did performance generalize to novel instances. However, even this successful transfer was restricted to those instances belonging to the birds' own training class (SCATTER), but not to the foreign class (COMPACT). That transfer performance was severely bound to common absolute stimulus characteristics was shown more directly by "tacitly" presenting "ambiguous" figures, or stimuli that closely resembled (symmetric) training patterns but whose symmetry content had now changed (those three modifications of each of five originally symmetric figures that now became asymmetric; see Figure 8).

T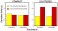his forced choice test revealed that generalization was solely the result of similarity rather than the possession of a symmetry concept. Figure 9 shows that all test stimuli were judged as similar to symmetric training stimuli (little deviation from symmetrical training stimuli, yellow bars), but as dissimilar to asymmetric training stimuli (large deviation from symmetrical training stimuli, red bars), regardless of their own symmetry type. Thus, irrespective of whether a test stimulus was symmetric or asymmetric, it was classified according to its similarity to the symmetric training stimulus it was derived from. Transfer was a matter of similarity and not of symmetry. Pigeons generalized, if at all, very conservatively (i.e., to only a small range around the stored templates, much like a cross-correlation-based template-matching system, Cerella, 1990).

The difference in the ability of the two groups of pigeons to store their respective training instances remains to be explained. If pigeons are living "photo-cameras", with large films that store the pictures they are presented without any further decomposition processes occurring, then such huge learning differences should not have occurred. Clearly, if one is only interested in models of categorization or conceptualization, then one can omit further discussion of this finding, or leave it to theories of pattern recognition and memory (as was done predominantly in the human literature on template matching). Those interested in the basic mechanisms underlying categorization in animals, however, require a more rigorous investigation of how pictures are processed in the animal's brain. This means that we will have to enter into a discussion of how visual objects or scenes are represented in the brain, and what aspects of these objects or scenes are used for discrimination or categorization tasks.

Exemplar-based categorization of birds versus mammals A very clear support for the exemplar view of visual categorization was found in an experiment by Cook et al. (1990) in which pigeons were required to learn a discrimination between line drawings depicting naturally occurring objects, namely birds and mammals. The primary evidence for this came from the uniform rates of discrimination acquisition among groups that were trained either with the S+ and S- stimuli unified by a category (the true categorization condition) or with reinforcement being uncorrelated with category membership (the pseudoconcept condition). Further evidence for learning each exemplar separately came from the significant facilitation of acquisition by using only 5 instances per category instead of 35 instances per category.  This difference in learning speed can be explained by a lack of within-category generalization, an important facet of relational or featural learning. Finally, the fact that transfer to novel category instances was determined not by the typicality of the pictures ('good' or 'poor' exemplars as assessed by human raters) but by the specific nature of the exemplars used during training is also in line with the exemplar view of categorization.  An important facet of this experiment is the successful specification of those aspects of the stimulus array that entered into the pigeons' memory. Using specific test variants of the pictures, the authors found that not the entire picture was stored, but only the animal figures themselves. From these figures, some features were not controlling the pigeons' classification behavior, like the 90 degree rotation or the reflection about the vertical axis. It seems as if the birds had selectively attended to specific aspects of the stimulus array and that they had decomposed the pictures into at least figure and ground. Such analytic processes, however, are perfectly in line with a more feature-based account of categorization and this apparent theoretical incompatibility points to a fundamental problem of perceptual learning: How do information-processing systems make determinations of similarity (Blough, 2001; Lea, 1984; Shepard, 1987)?

In principle, we may distinguish between item-specific and category-specific aspects of the stimuli. The first ones are needed to discriminate between instances of the same class; the second ones are needed to discriminate between instances of different classes. Differential within- versus between-class generalization is commonly considered as a key feature of visual categorization in animals (Wasserman & Astley, 1994). If no category-specific information is available as a kind of relational information about common properties of a category, then classification learning will be restricted to learning about each individual stimulus separately and distinctly. If it were available, learning to use it will significantly facilitate classification, both in terms of acquisition and transfer to novel instances. The facilitation of classification is due to intra-class generalization, that is transfer to novel instances of the same class is mediated by generalization or item similarity to the previously learned exemplars. The classic procedure to disclose learning about category-specific features is the pseudoconcept task which involves the arbitrary assignment of category (for example "fish", Herrnstein & de Villiers, 1980) and non-category exemplars ("non-fish" in this example) to positive and negative classes, respectively. Lea and Ryan (1990) called this the "perverse pseudoconcept task" in order to distinguish it from the alternative "random pseudoconcept task" in which no 'concept' exists within the stimulus set).

A number of categorization experiments involving such pseudoconcept tests have successfully shown that pigeons learn about category-specific information in contrast or in addition to item-specific information (Herrnstein & de Villiers, 1980; Edwards, & Honig, 1987; Pearce, 1988; Wasserman, Kiedinger & Bhatt, 1988). On the other hand, using a similar procedure, some authors have found differences in acquisition rate and concluded that the animals achieved a discrimination by learning only about the specific stimuli in the acquisition phase (Vaughan & Greene, 1983; Schrier, Angarella & Povar, 1984; Cook, Wright & Kendrick, 1990). 

A very reasonable suggestion brought forward by Cook et al. (1990, also see sidebar) is that categorical discriminations may consist of two phases, a "stimulus learning" and a "concept" phase. The first would involve only learning about the exemplars by attending to the item-specific information that distinguishes them from all other stimuli. The second phase, in which category-specific information is extracted, may then follow. In cases in which it doesn't, as in our symmetry experiment above, true open-ended categorization as a means of minimizing memory requirements is not achieved. It is fair to say, that absolute, data-driven, exemplar-based strategies of categorization are a plausible alternative to more relational and analytic processing mechanisms, especially from an engineering point of view (Cook et al., 1990). However, the relevance for pigeons and other animals in the wild remains to be specified (see an extensive discussion of this issue in Huber, 1995, 1999).

Next Section: Feature Learning