A series of studies by Biederman and colleagues have indicated that geons may be the fundamental local features of objects (Biederman, 1987; Biederman & Blickle, 1985; Biederman, Ju, & Clapper, 1985). Kirkpatrick-Steger, Wasserman, and Biederman (1998) examined whether geons are important to pigeons in recognizing line drawings. Pigeons were first trained to discriminate among four drawings of a watering can, an iron, a desk lamp, and a sailboat using the four-key choice procedure. Each of the training stimuli contained four geons.

Altered Geons
Testing  Type	Can	Handle	Nozzle	Spout
Moved  Geon
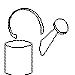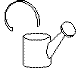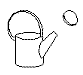Deleted  Geon
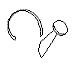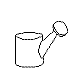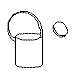Retained  Geon

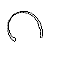Once the pigeons had attained a high level of accuracy on the training procedure, they were tested with versions of the objects in which one or three components were deleted or a single component was moved away from the other three. To examine the contribution of each individual component, the effect of moving or deleting a geon was contrasted with the effect of presenting the geon by itself. If an individual geon was particularly important for object recognition, then there would be maintained accuracy when the geon was presented alone and decremented accuracy when the geon was deleted. Moving a geon serves as a contrast to deleting the geon, because the geon is still present on the screen, but the location is altered relative to the other three.

All four pigeons continued to discriminate the original drawings at a high level of accuracy in these tests. When a single geon was either moved or deleted, there was no apparent effect on recognition accuracy. In contrast, deleting three geons produced a significant disruption in accuracy scores, but performance was still above the chance level of 25%. The pattern of results is consistent with studies of recognition of partial objects in humans, where the principle of three-geon sufficiency is observed: If two or three of an object's geons are present in the correct spatial organization, then object recognition will occur as normal, but if only a single geon is present, recognition suffers (Biederman, Ju, & Clapper, 1985). Recognition-by-components (RBC; Biederman, 1987) predicts that the principle of three-geon sufficiency will hold, provided that the spatial organization of the components is preserved. This feature of RBC allows for recognition of objects, even when they are partially occluded from view. 

Inspection of the accuracy scores to the individual drawings in individual birds revealed uniformly high performance to both the 1-moved and 1-deleted drawings. On the other hand, accuracy scores to the individual 3-deleted drawings were not uniform, as seen in the table below. For example, geons such as the spout of the watering can, the knob of the iron, and the curved sail of the sailboat were discriminated poorly when displayed alone. The best-discriminated geons for each training object were the handle of the watering can, the cord of the iron, the base of the desk lamp, and the hull of the sailboat. While some geons produced fairly consistent results across birds, others produced quite inconsistent results. For example, the can of the watering can was responded to above chance in Birds 1 and 4, but responding was near 0% correct in the other two birds. The results indicate that some geons may be especially distinctive and can activate a stored representation of an object by themselves, while others may be incapable of supporting accurate recognition alone.

Bird	Original	Retained Geon
1 2 3 4	Watering Can 96.9* 78.1* 93.8* 78.1*	Can 62.5* 0.0 12.5 75.0*	Handle 75.0* 37.5 75.0* 75.0*	Nozzle 62.5* 37.5 12.5 25.0	Spout 37.5 12.5 25.0 25.0
1 2 3 4	Iron 81.3* 96.9* 87.5* 68.8*	Base 25.0 25.0 75.0* 62.5*	Cord 50.0 75.0* 62.5* 75.0*	Handle 0.0 62.5* 50.0 37.5	Knob 12.5 12.5 25.0 25.0
1 2 3 4	Desk Lamp 93.8* 93.8* 90.6* 93.8*	Base 75.0* 87.5* 100.0* 75.0*	Fixture 87.5* 50.0 50.0 37.5	Shade 75.0* 62.5* 50.0 87.5*	Stem 62.5* 37.5 87.5* 75.0
1 2 3 4	Sailboat 100.0* 93.8* 81.3* 56.3*	C. Sail 0.0 50.0 25.0 0.0	Hull 100.0* 100.0* 37.5 37.5	Mast 12.5 75.0* 0.0 12.5	T. Sail 75.0* 87.5* 50.0 37.5

The above results stand in contrast to Particulate feature theory (Cerella, 1986), which predicts that the loss of any parts of an object would produce a decrement in accuracy. The results do appear indicate that geons were important for recognition (but they don't indicate that geons are the only important local features). The fact that the principle of three-geon sufficiency (Biederman, 1987) was apparent in pigeon's recognition capabilities lends further support to the notion that geons are important componential units of objects.

Van Hamme, Wasserman, and Biederman (1992) have provided an additional demonstration that geons may be fundamental components for object recognition in pigeons. They trained pigeons to discriminate among four line drawings of objects, each of which had half of the contours and vertices missing. The contour-deleted objects still contained sufficient information for the parsing of the relevant geons at regions of concavity. When the pigeons were later tested with objects that contained the complimentary set of contours, substantial generalization was observed. These results are quite remarkable given that the complimentary-contour images contain none of the local features present in the original images. Clearly, the pigeons must have learned more about the contour-deleted objects than the strict pieces of contour. RBC would argue that the process that mediates the recognition of complimentary-contour images is the same process that recognizes intact images: provided that the geons and their spatial organizations can be determined from the more limited contour and vertice information, then both a contour-deleted and its complimentary image will activate the same structural description.

The fact that a subset of single geons were capable of supporting accurate recognition when they were presented alone (3-deletion) is somewhat problemmatic for RBC because only limited featural information and no organizational information was available in the 3-deleted drawings. The maintained accuracy with single geons could be due to the use of only four training objects. In this situation, there were several geons that were unique to particular objects, which may have facilitated attention to the individual geons. What remains to be determined is the relative importance of the components and their spatial organization (see what/where experiment).

Next Section: Relative Importance of Geons and Interrelations